DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Coupled Strings Eigenanalysis

In §6.12.2, general coupling of horizontal and vertical planes of vibration in an ideal string was considered. This eigenanalysis will now be applied here to obtain formulas for the damping and mode tuning caused by the coupling of two identical strings at a bridge. This is the case that arises in pianos [543].

The general formula for linear, time-invariant coupling of two strings can be written, in the frequency domain, as

$\displaystyle \left[\begin{array}{c} V_1^-(s) \\ [2pt] V_2^-(s) \end{array}\rig... ... \left[\begin{array}{c} V_1^+(s) \\ [2pt] V_2^+(s) \end{array}\right]. \protect$ (C.115)

Filling in the elements of this coupling matrix $ \mathbf{H}_c$ from the results of §C.13.1, we obtain

$\displaystyle \mathbf{H}_c(s) = \left[\begin{array}{cc} 1-H_b(s) & -H_b(s) \\ [2pt] -H_b(s) & 1-H_b(s) \end{array}\right] $

where

$\displaystyle H_b(s) = \frac{2}{2+\tilde{R}_b}. $

Here $ \tilde{R}_b\isdef R_b/R$ is the bridge impedance divided by the string impedance. Treating $ \mathbf{H}_c(s)$ as a constant complex matrix for each fixed $ s$, the eigenvectors are foundC.10to be

$\displaystyle \underline{e}_1 = \left[\begin{array}{c} 1 \\ [2pt] 1 \end{array}... ...uad \underline{e}_2 = \left[\begin{array}{c} 1 \\ [2pt] -1 \end{array}\right], $

respectively, and the eigenvalues are

$\displaystyle \lambda_1(s) = 1 - 2H_b(s), \qquad \lambda_2 = 1. $

Note that only one eigenvalue depends on $ s=j\omega$, and neither eigenvector is a function of $ s$.

We conclude that ``in-phase vibrations'' see a longer effective string length, lengthened by the phase delay of

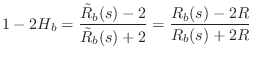
$\displaystyle 1-2H_b = \frac{\tilde{R}_b(s)-2}{\tilde{R}_b(s)+2} = \frac{R_b(s)-2R}{R_b(s)+2R} $

which is the reflectance seen from two in-phase strings each having impedance $ R$. This makes physical sense because the in-phase vibrations will move the bridge in the vertical direction, causing more rapid decay of the in-phase mode.

We similarly conclude that the ``anti-phase vibrations'' see no length correction at all, because the bridge point does not move at all in this case. In other words, any bridge termination at a point is rigid with respect to anti-phase vibration of the two strings connected to that point.

The above analysis predicts that, in ``stiffness controlled'' frequency intervals (in which the bridge ``looks like a damped spring''), the ``initial fast decay'' of a piano note should be a measurably flatter than the ``aftersound'' which should be exactly in tune as if the termination were rigid.

Next Section:
The Rectilinear 2D Mesh
Previous Section:
Two Ideal Strings Coupled at an Impedance