DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

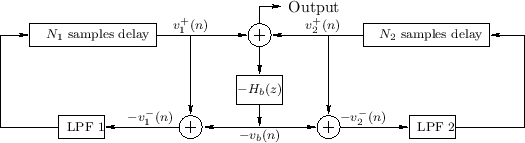
Two Ideal Strings Coupled at an Impedance

A diagram for the two-string case is shown in Fig. C.30. This situation is a special case of the loaded waveguide junction, Eq.$ \,$(C.98), with the number of waveguides being $ N=2$, and the junction load being the transverse driving-point impedance $ R_b(s)$ where the string drives the bridge. If the bridge is passive, then its impedance $ R_b(s)$ is a positive real function (see §C.11.2). For a direct derivation, we need only observe that (1) the string velocities of each string endpoint must each be equal to the velocity of the bridge, or $ v_1 = v_2 = v_b$, and (2) the sum of forces of both strings equals the force applied to the bridge: $ f_b = f_1 + f_2$. The bridge impedance relates the force and velocity of the bridge via $ F_b(s) = R_b(s) V_b(s)$. Expanding into traveling wave components in the Laplace domain, we have

$\displaystyle R_b(s) V_b(s)$ $\displaystyle =$ $\displaystyle F_b(s) = F_1(s) + F_2(s)$ (C.108)
  $\displaystyle =$ $\displaystyle [F^+_1(s) + F^-_1(s)] + [F^+_2(s) + F^-_2(s)]$ (C.109)
  $\displaystyle =$ $\displaystyle R_1 \{V^+_1(s) - [V_b(s) - V^+_1(s)] \}$ (C.110)
  $\displaystyle \,+\,$ $\displaystyle R_2 \{V^+_2(s) - [V_b(s) - V^+_2(s)]\}$ (C.111)

or

$\displaystyle V_b(s) = H_b(s) [ R_1 V^+_1(s) + R_2 V^+_2(s) ] $

where $ R_i$ is the wave impedance of string $ i$, and

$\displaystyle H_b(s)\isdef \frac{2}{R_b(s) + R_1 + R_2} $

Thus, in the time domain, the incoming velocity waves are scaled by their respective wave impedances, summed together, and filtered according to the transfer function $ H_b(s) = 2/[R_b(s) + R_1 + R_2]$ to obtain the velocity of the bridge $ v_b(t)$.

Given the filter output $ v_b(t)$, the outgoing traveling velocity waves are given by

$\displaystyle v^-_1(t)$ $\displaystyle =$ $\displaystyle v_b(t) - v^+_1(t)$ (C.112)
$\displaystyle v^-_2(t)$ $\displaystyle =$ $\displaystyle v_b(t) - v^+_2(t) \ $ (C.113)

Thus, the incoming waves are subtracted from the bridge velocity to get the outgoing waves.

Since $ V^-_2(s) = H_b(s) R_1 V^+_1(s) = H_b(s) F^+_1(s)$ when $ V^+_2(s) = 0$, and vice versa exchanging strings $ 1$ and $ 2$, $ H_b$ may be interpreted as the transmission admittance filter associated with the bridge coupling. It can also be interpreted as the bridge admittance transfer function from every string, since its output is the bridge velocity resulting from the sum of incident traveling force waves.

A general coupling matrix contains a filter transfer function in each entry of the matrix. For $ N$ strings, each conveying a single type of wave (e.g., horizontally polarized), the general linear coupling matrix would have $ N^2$ transfer-function entries. In the present formulation, only one transmission filter is needed, and it is shared by all the strings meeting at the bridge. It is easy to show that the shared transmission filter for two coupled strings generalizes to $ N$ strings coupled at a common bridge impedance: From (C.98), we have

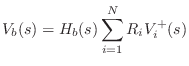
$\displaystyle V_b(s) = H_b(s) \sum_{i=1}^N R_i V^{+}_i(s) $

where

$\displaystyle H_b(s) = \frac{2}{R_b(s) + \sum_{i=1}^N R_i} $

Thus, $ H_b(s)$ is the shared portion of the bridge filtering, leaving only a scaling according to relative impedance to be done in each branch.

The above sequence of operations is formally similar to the one multiply scattering junction frequently used in digital lattice filters [297]. In this context, it would be better termed the ``one-filter scattering termination.''

When the two strings are identical (as would be appropriate in a model for coupled piano strings), the computation of bridge velocity simplifies to

$\displaystyle V_b(s) = H_b(s) [V^+_1(s) + V^+_2(s)] \protect$ (C.114)

where $ H_b(s)\isdef 2/[2 + R_b(s)/R]$ is the velocity transmission filter. In this case, the incoming velocities are simply summed and fed to the transmission filter which produces the bridge velocity at its output. A commuted simulation diagram appears in Fig. C.31.

Figure C.31: General linear coupling of two equal-impedance strings using a common bridge filter.
\includegraphics{eps/fcouplednompy}

Note that a yielding bridge introduces losses into all attached strings. Therefore, in a maximally simplified implementation, all string loop filters (labeled LPF$ _1$ and LPF$ _2$ in Fig.C.31) may be eliminated, resulting in only one filter--the transmission filter--serving to provide all losses in a coupled-string simulation. If that transmission filter has no multiplies, then neither does the entire multi-string simulation.

Next Section:
Coupled Strings Eigenanalysis
Previous Section:
Positive Real Functions