DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Delay-Line Interpolation Summary

The most commonly used closed-form methods for delay-line interpolation may be summarized by the following table:

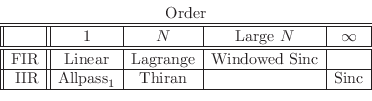
\begin{displaymath} \begin{array}{c} \mbox{Order}\\ \begin{array}{\vert\vert r\... ...\mbox{Thiran} & & \mbox{Sinc} \\ \hline \end{array}\end{array}\end{displaymath}

In the first column, we have linear and first-order allpass interpolation, as discussed above in sections §4.1.1 and §4.1.2, respectively. These are the least-expensive methods computationally, and they find wide use, especially in audio applications with large sampling rates. While linear and first-order allpass interpolation cost the same, only linear interpolation offers ``random access mode''. That is, since the interpolated signal is a (finite) linear combination of known samples, the signal can be evaluated at any arbitrary time within the range of known samples -- the interpolation can ``jump around'' as desired. On the other hand, allpass interpolation has no gain error, so it may preferred inside a feedback loop to provide slowly varying fractional delay filtering.

In the second column -- $ N$th-order interpolation -- we list Lagrange for the FIR case (top) and Thiran for the IIR case (bottom), and these are introduced in §4.2 and §4.3, respectively. Lagrange and Thiran interpolators, properly implemented, enjoy the following advantages:

  • Gain bounded by 1 at all frequencies
  • Coefficients known in closed form as a function of desired delay
  • Maximally flat at low frequencies:
    -
    Lagrange: maximally flat frequency response at dc
    -
    Thiran: maximally flat group delay at dc

In the high-order FIR case, one should also consider ``windowed sinc'' interpolation (introduced in §4.4) as an alternative to Lagrange interpolation. In fact, as discussed in §4.2.16, Lagrange interpolation is a special case of windowed-sinc interpolation in which a scaled binomial window is used. By choosing different windows, optimalities other than ``maximally flat at dc'' can be achieved.

In the most general $ N$th-order case, the interpolation-filter impulse response may be designed to achieve any optimality objective, such as Chebyshev optimality (Fig.4.11). That is, design a digital filter (FIR or IIR) that approximates

$\displaystyle H_\Delta\left(e^{j\omega T}\right) = e^{-j\omega\Delta T},\quad \Delta = \hbox{Desired delay in samples} $

optimally in some sense, with coefficients tabulated over a range of $ \Delta$ samples (and interpolated on lookup). Tabulated filter-designs of this nature, while generally giving the best interpolation quality, are not included in the above table because the filter-coefficients are not known in closed form.

FIR interpolators have the advantage that they can be used in ``random access'' mode. IIR interpolators, on the other hand, require a sequential stream of input samples and produce a sequential stream of interpolated signal samples (typically implementing a fractional delay). In IIR fractional-delay filters, the fractional delay must change slowly relative to the IIR duration.

Finally, we note in the last column of the above table that if ``order is no object'' ( $ N\to\infty$), then the ideal bandlimited-interpolator impulse-response is simply a sampled sinc function, as discussed in §4.4.

Next Section:
Variable Delay Lines
Previous Section:
Windowed Sinc Interpolation