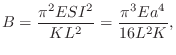DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Dispersion Filter-Design

In the context of a digital waveguide string model, dispersion associated with stiff strings can be supplied by an allpass filter in the basic feedback loop. Methods for designing dispersion allpass filters were summarized in §6.11.3. In this section, we are mainly concerned with how to specify the desired dispersion allpass filter for piano strings.

Perceptual studies regarding the audibility of inharmonicity in stringed instrument sounds [211] indicate that the just noticeable coefficient of inharmonicity is given approximately by

$\displaystyle B_{\mbox{thresh}} = \exp[2.54\,\log(f_0)-24.6] \protect$ (10.31)

where $ f_0$ is the fundamental frequency of the string vibration in hertz, and $ B$--the so-called coefficient of inharmonicity--affects the $ n$th partial overtone tuning via

$\displaystyle f_n = nf_0\sqrt{1+Bn^2}. \protect$ (10.32)

For a stiff string with Young's modulus $ E$, radius $ a$, length $ L$, and tension $ K$, the coefficient of inharmonicity $ B$ is predicted from theory [144, p. 65],[211] to be

$\displaystyle B = \frac{\pi^2 E S I^2}{K L^2} = \frac{\pi^3 E a^4}{16 L^2 K}, \protect$ (10.33)

where $ S=\pi a^2$ is the string cross-sectional area, and $ I=a/2$ is the radius of gyration of the string cross-section (see §B.4.9).

In general, when designing dispersion filters for vibrating string models, it is highly cost-effective to obtain an allpass filter which correctly tunes only the lowest-frequency partial overtones, where the number of partials correctly tuned is significantly less than the total number of partials present, as in [384].

Application of the method of [2] to piano-string dispersion-filter design is reported in [1].

A Faust implementation of a closed-form expression [367] for dispersion allpass coefficients as a function of inharmonicity coefficient $ B$ may be found in the function piano_dispersion_filter within effect.lib.

Next Section:
Nonlinear Piano-String Synthesis
Previous Section:
Damping-Filter Design