Equations of Motion for Rigid Bodies

Free Books Physical Audio Signal Processing

We are now ready to write down the general equations of motion for rigid bodies in terms of for the center of mass and $\tau=I\alpha$ for the rotation of the body about its center of mass.

As discussed above, it is useful to decompose the motion of a rigid body into

(1): the linear velocity $\underline{v}$ of its center of mass, and
(2): its angular velocity $\underline{\omega}$ about its center of mass.

The linear motion is governed by Newton's second law $\underline{f}=M\dot{\underline{v}}$ , where is the total mass, $\underline{v}$ is the velocity of the center-of-mass, and $\underline{f}$ is the sum of all external forces on the rigid body. (Equivalently, $\underline{f}$ is the sum of the radial force components pointing toward or away from the center of mass.) Since this is so straightforward, essentially no harder than dealing with a point mass, we will not consider it further.

The angular motion is governed the rotational version of Newton's second law introduced in §B.4.19:

$\displaystyle \underline{\tau}\eqsp \dot{\underline{L}} \eqsp \mathbf{I}\,\dot{\underline{\omega}} \eqsp \mathbf{I}\,\dot{\underline{\omega}} \protect$

(B.29)

where $\tau$ is the vector torque defined in Eq. $\,$ (B.27), $\underline{L}$ is the angular momentum, $\mathbf{I}$ is the mass moment of inertia tensor, and $\underline{\omega}$ is the angular velocity of the rigid body about its center of mass. Note that if the center of mass is moving, we are in a moving coordinate system moving with the center of mass (see next section). We may call $\underline{L}$ the intrinsic momentum of the rigid body, i.e., that in a coordinate system moving with the center of the mass. We will translate this to the non-moving coordinate system in §B.4.20 below.

The driving torque $\underline{\tau}$ is given by the resultant moment of the external forces, using Eq. $\,$ (B.27) for each external force to obtain its contribution to the total moment. In other words, the external moments (tangential forces times moment arms) sum up for the net torque just like the radial force components summed to produce the net driving force on the center of mass.

Body-Fixed and Space-Fixed Frames of Reference

Rotation is always about some (instantaneous) axis of rotation that is free to change over time. It is convenient to express rotations in a coordinate system having its origin ( $\underline{0}$ ) located at the center-of-mass of the rigid body (§B.4.1), and its coordinate axes aligned along the principal directions for the body (§B.4.16). This body-fixed frame then moves within a stationary space-fixed frame (or ``star frame'').

In Eq. $\,$ (B.29) above, we wrote down Newton's second law for angular motion in the body-fixed frame, i.e., the coordinate system having its origin at the center of mass. Furthermore, it is simplest ( $\mathbf{I}$ is diagonal) when its axes lie along principal directions (§B.4.16).

As an example of a local body-fixed coordinate system, consider a spinning top. In the body-fixed frame, the ``vertical'' axis coincides with the top's axis of rotation (spin). As the top loses rotational kinetic energy due to friction, the top's rotation-axis precesses around a circle, as observed in the space-fixed frame. The other two body-fixed axes can be chosen as any two mutually orthogonal axes intersecting each other (and the spin axis) at the center of mass, and lying in the plane orthogonal to the spin axis. The space-fixed frame is of course that of the outside observer's inertial frame^B.28in which the top is spinning.

Angular Motion in the Space-Fixed Frame

Let's now consider angular motion in the presence of linear motion of the center of mass. In general, we have [270]

$\displaystyle \underline{L}\eqsp \sum \underline{x}\times \underline{p}$

where the sum is over all mass particles in the rigid body, and $\underline{p}$ denotes the vector linear momentum for each particle. That is, the angular momentum is given by the tangential component of the linear momentum times the associated moment arm. Using the chain rule for differentiation, we find

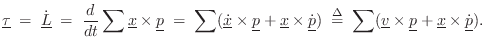
$\displaystyle \underline{\tau}\eqsp \dot{\underline{L}} \eqsp \frac{d}{dt}\sum ... ...m (\underline{v}\times\underline{p}+ \underline{x}\times \dot{\underline{p}}).$

However, $\underline{v}\times \underline{p}=\underline{v}\times m\underline{v}=\underline{0}$ , so that

$\displaystyle \underline{\tau}\eqsp \dot{\underline{L}} \eqsp \sum \underline{x}\times \dot{\underline{p}} \eqsp \sum \underline{x}\times \underline{f}$

which is the sum of moments of all external forces.

Euler's Equations for Rotations in the Body-Fixed Frame

Suppose now that the body-fixed frame is rotating in the space-fixed frame with angular velocity $\underline{\omega}$ . Then the total torque on the rigid body becomes [270]

$\displaystyle \underline{\tau}\eqsp \dot{\underline{L}} + \underline{\omega}\times \underline{L}. \protect$

(B.30)

Similarly, the total external forces on the center of mass become

$\displaystyle \underline{f}\eqsp \dot{\underline{p}} + \underline{\omega}\times\underline{p}.$

If the body-fixed frame is aligned with the principal axes of rotation (§B.4.16), then the mass moment of inertia tensor is diagonal, say $\mathbf{I}=$ diag

. In this frame, the angular momentum is simply

$\displaystyle \underline{L}\eqsp \left[\begin{array}{c} I_1\omega_1 \\ [2pt] I_2\omega_2 \\ [2pt] I_3\omega_3\end{array}\right]$

so that the term $\underline{\omega}\times\underline{L}$ becomes (cf. Eq. $\,$ (B.15))

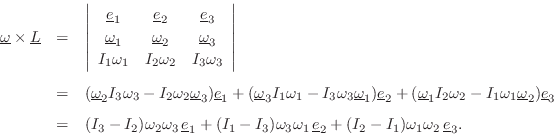
$\begin{eqnarray*} \underline{\omega}\times\underline{L}&=& \left\vert \begin{arr... ...1\,\underline{e}_2 + (I_2-I_1)\omega_1\omega_2\,\underline{e}_3. \end{eqnarray*}$

Substituting this result into Eq. $\,$ (B.30), we obtain the following equations of angular motion for an object rotating in the body-fixed frame defined by its three principal axes of rotation:

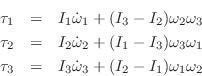
$\begin{eqnarray*} \tau_1 &=& I_1 \dot{\omega}_1 + (I_3-I_2)\omega_2\omega_3\\ \... ...a_1\\ \tau_3 &=& I_3 \dot{\omega}_3 + (I_2-I_1)\omega_1\omega_2 \end{eqnarray*}$

These are call Euler's equations:^B.29Since these equations are in the body-fixed frame, is the mass moment of inertia about principal axis , and $\omega_i$ is the angular velocity about principal axis .

Examples

For a uniform sphere, the cross-terms disappear and the moments of inertia are all the same, leaving $\tau_i=I\omega_i$ , for . Since any three orthogonal vectors can serve as eigenvectors of the moment of inertia tensor, we have that, for a uniform sphere, any three orthogonal axes can be chosen as principal axes.

For a cylinder that is not spinning about its axis, we similarly obtain two uncoupled equations $\tau_i=I\omega_i$ , for , given $\omega_3=\tau_3=0$ (no spin). Note, however, that if we replace the circular cross-section of the cylinder by an ellipse, then $I_1\ne I_2$ and there is a coupling term that drives $\dot{\omega}_3$ (unless $\tau_3$ happens to cancel it).