DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

FDN Stability

Stability of the FDN is assured when some norm [451] of the state vector $ \mathbf{x}(n)$ decreases over time when the input signal is zero [220, ``Lyapunov stability theory'']. That is, a sufficient condition for FDN stability is

$\displaystyle \left\Vert\,\mathbf{x}(n+1)\,\right\Vert < \left\Vert\,\mathbf{x}(n)\,\right\Vert, \protect$ (3.12)

for all $ n\geq0$, where $ \left\Vert\,\mathbf{x}(n)\,\right\Vert$ denotes the norm of $ \mathbf{x}(n)$, and

$\displaystyle \mathbf{x}(n+1) = \mathbf{A}\left[\begin{array}{c} x_1(n-M_1) \\ [2pt] x_2(n-M_2) \\ [2pt] x_3(n-M_3)\end{array}\right]. $

Using the augmented state-space analysis mentioned above, the inequality of Eq.$ \,$(2.12) holds under the $ L2$ norm [451] whenever the feedback matrix $ \mathbf{A}$ in Eq.$ \,$(2.6) satisfies [473]

$\displaystyle \left\Vert\,\mathbf{A}\mathbf{x}\,\right\Vert _2 < \left\Vert\,\mathbf{x}\,\right\Vert _2 \protect$ (3.13)

for all $ \mathbf{x}$, where $ \left\Vert\,\cdot\,\right\Vert _2$ denotes the $ L2$ norm, defined by

$\displaystyle \left\Vert\,\mathbf{x}\,\right\Vert _2 \isdef \sqrt{x_1^2+x_2^2+\dots+x_N^2}. $

In other words, stability is guaranteed when the feedback matrix decreases the $ L2$ norm of its input vector.

The matrix norm corresponding to any vector norm $ \vert\vert\,\cdot\,\vert\vert $ may be defined for the matrix $ \mathbf{A}$ as

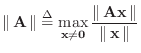
$\displaystyle \left\Vert\,\mathbf{A}\,\right\Vert \isdef \max_{\mathbf{x}\neq \... ...\Vert\,\mathbf{A}\mathbf{x}\,\right\Vert}{\left\Vert\,\mathbf{x}\,\right\Vert} $

where $ \left\Vert\,\mathbf{x}\,\right\Vert$ denotes the norm of the vector $ \mathbf{x}$. In other words, the matrix norm ``induced'' by a vector norm is given by the maximum of $ \vert\vert\,\mathbf{A}\mathbf{x}\,\vert\vert $ over all unit-length vectors $ \mathbf{x}$ in the space. When the vector norm is the $ L2$ norm, the induced matrix norm is often called the spectral norm. Thus, Eq.$ \,$(2.13) can be restated as

$\displaystyle \left\Vert\,\mathbf{A}\,\right\Vert _2 < 1 \protect$ (3.14)

where $ \left\Vert\,\mathbf{A}\,\right\Vert _2$ denotes the spectral norm of $ \mathbf{A}$.

It can be shown [167] that the spectral norm of a matrix $ \mathbf{A}$ is given by the largest singular value of $ \mathbf{A}$ (`` $ \left\Vert\,\mathbf{A}\,\right\Vert _2=\sigma_1(\mathbf{A})$''), and that this is equal to the square-root of the largest eigenvalue of $ \mathbf{A}\mathbf{A}^T$, where $ \mathbf{A}^T$ denotes the matrix transpose of the real matrix $ \mathbf{A}$.3.11

Since every orthogonal matrix $ \mathbf{Q}$ has spectral norm 1,3.12 a wide variety of stable feedback matrices can be parametrized as

$\displaystyle \mathbf{A}= {\bm \Gamma}\mathbf{Q} $

where $ \mathbf{Q}$ is any orthogonal matrix, and $ {\bm \Gamma}$ is a diagonal matrix having entries less than 1 in magnitude:

$\displaystyle {\bm \Gamma}= \left[ \begin{array}{cccc} g_1 & 0 & \dots & 0\\ 0... ...\\ 0 & 0 & \dots & g_N \end{array}\right], \quad \left\vert g_i\right\vert<1. $

An alternative stability proof may be based on showing that an FDN is a special case of a passive digital waveguide network (derived in §C.15). This analysis reveals that the FDN is lossless if and only if the feedback matrix $ \mathbf{A}$ has unit-modulus eigenvalues and linearly independent eigenvectors.

Next Section:
Allpass from Two Combs
Previous Section:
Single-Input, Single-Output (SISO) FDN