Free Books    Physical Audio Signal Processing  

Allpass from Two Combs

Figure 2.30: A combined feedback/feedforward comb filter which gives an allpass filter when $ b_0 = a_M$.
\includegraphics{eps/fbffcf}

An allpass filter can be defined as any filter having a gain of $ 1$ at all frequencies (but typically different delays at different frequencies).

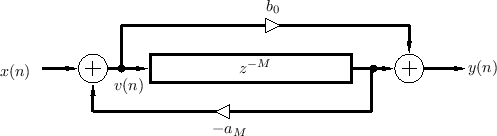
It is well known that the series combination of a feedforward and feedback comb filter (having equal delays) creates an allpass filter when the feedforward coefficient is the negative of the feedback coefficient.

Figure 2.30 shows a combination feedforward/feedback comb filter structure which shares the same delay line.3.13 By inspection of Fig.2.30, the difference equation is

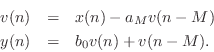
\begin{eqnarray*} v(n) &=& x(n) - a_M v(n-M)\\ y(n) &=& b_0 v(n) + v(n-M). \end{eqnarray*}

This can be recognized as a digital filter in direct form II [449]. Thus, the system of Fig.2.30 can be interpreted as the series combination of a feedback comb filter (Fig.2.24) taking $ x(n)$ to $ v(n)$ followed by a feedforward comb filter (Fig.2.23) taking $ v(n)$ to $ y(n)$. By the commutativity of LTI systems, we can interchange the order to get

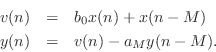
\begin{eqnarray*} v(n) &=& b_0 x(n) + x(n-M)\\ y(n) &=& v(n) - a_M y(n-M). \end{eqnarray*}

Substituting the right-hand side of the first equation above for $ v(n)$ in the second equation yields more simply

$\displaystyle y(n) = b_0 x(n) + x(n-M) - a_M y(n-M). \protect$ (3.15)

This can be recognized as direct form I [449], which requires $ 2M$ delays instead of $ M$; however, unlike direct-form II, direct-form I cannot suffer from ``internal'' overflow--overflow can happen only at the output.

The coefficient symbols $ b_0$ and $ a_M$ here have been chosen to correspond to standard notation for the transfer function

$\displaystyle H(z) = \frac{b_0 + z^{-M}}{1 + a_M z^{-M}}. $

The frequency response is obtained by setting $ z = e^{j\omega T}$, where $ \omega $ denotes radian frequency and $ T$ denotes the sampling period in seconds [449]. For an allpass filter, the frequency magnitude must be the same for all $ \omega\in[-\pi/T,\pi/T]$.

An allpass filter is obtained when $ b_0 = \overline{a_M}$, or, in the case of real coefficients, when $ b_0 = a_M$. To see this, let $ a\isdef a_M=\overline{b_0}$. Then we have

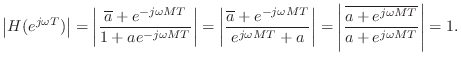
$\displaystyle \left\vert H(e^{j\omega T})\right\vert = \left\vert\frac{\overli... ...eft\vert\frac{\overline{a + e^{j\omega MT}}}{a+e^{j\omega MT}}\right\vert = 1. $

Next Section:
Nested Allpass Filters
Previous Section:
FDN Stability