DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

FDNs as Digital Waveguide Networks

This section supplements §2.7 on Feedback Delay Networks in the context of digital waveguide theory. Specifically, we review the interpretation of an FDN as a special case of a digital waveguide network, summarizing [463,464,385].

Figure C.36 illustrates an $ N$-branch DWN. It consists of a single scattering junction, indicated by a white circle, to which $ N$ branches are connected. The far end of each branch is terminated by an ideal non-inverting reflection (black circle). The waves traveling into the junction are associated with the FDN delay line outputs $ x_i(n-M_i)$, and the length of each waveguide is half the length of the corresponding FDN delay line $ M_i$ (since a traveling wave must traverse the branch twice to complete a round trip from the junction to the termination and back). When $ M_i$ is odd, we may replace the reflecting termination by a unit-sample delay.

Figure C.36: Waveguide network consisting of a single scattering junction, indicated by an open circle, to which $ N$ branches are connected. The far end of each branch is terminated by an ideal, non-inverting reflection.
\includegraphics[scale=0.5]{eps/DWN}

Lossless Scattering

The delay-line inputs (outgoing traveling waves) are computed by multiplying the delay-line outputs (incoming traveling waves) by the $ N\times N$ feedback matrix (scattering matrix) $ \mathbf{A}= [a_{i,j}]$. By defining $ p^+_i= x_i(n-M_i)$, $ p^-_i= x_i(n)$, we obtain the more usual DWN notation

$\displaystyle \mathbf{p}^- = \mathbf{A}\mathbf{p}^+$ (C.119)

where $ \mathbf{p}^+$ is the vector of incoming traveling-wave samples arriving at the junction at time $ n$, $ \mathbf{p}^-$ is the vector of outgoing traveling-wave samples leaving the junction at time $ n$, and $ \mathbf{A}$ is the scattering matrix associated with the waveguide junction.

The junction of $ N$ physical waveguides determines the structure of the matrix $ \mathbf{A}$ according to the basic principles of physics.

Considering the parallel junction of $ N$ lossless acoustic tubes, each having characteristic admittance $ \Gamma_j=1/R_j$, the continuity of pressure and conservation of volume velocity at the junction give us the following scattering matrix for the pressure waves [433]:

$\displaystyle {\bf A} = \left[ \begin{array}{rrrr} \frac{2 \Gamma_{1}}{\Gamma_J... ...{2}}{\Gamma_J} & \dots & \frac{2 \Gamma_{N}}{\Gamma_J} -1\\ \end{array} \right]$ (C.120)

where

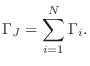$\displaystyle \Gamma_J = \sum_{i=1}^N\Gamma_{i}.$ (C.121)

Equation (C.121) can be derived by first writing the volume velocity at the $ j$-th tube in terms of pressure waves as $ v_j = (p_j^+ - p_j^-)\Gamma_j$. Applying the conservation of velocity we can find the expression

$\displaystyle p = 2 \sum_{i=1}^{N}\Gamma_{i} p_i^+ / \Gamma_J $

for the junction pressure. Finally, if we express the junction pressure as the sum of incoming and outgoing pressure waves at any branch, we derive (C.121). See §C.12 for further details.

Normalized Scattering

For ideal numerical scaling in the $ L_2$ sense, we may choose to propagate normalized waves which lead to normalized scattering junctions analogous to those encountered in normalized ladder filters [297]. Normalized waves may be either normalized pressure $ \tilde{p}_j^+ = p_j^+\sqrt{\Gamma_i}$ or normalized velocity $ \tilde{v}_j^+ = v_j^+/\sqrt{\Gamma_i}$. Since the signal power associated with a traveling wave is simply $ {\cal P_j^+} = (\tilde{p}_j^+)^2 = (\tilde{v}_j^+)^2$, they may also be called root-power waves [432]. Appendix C develops this topic in more detail.

The scattering matrix for normalized pressure waves is given by

$\displaystyle \tilde{\mathbf{A}}= \left[ \begin{array}{llll} \frac{2 \Gamma_{1}... ..._{2}}}{\Gamma_J} & \dots & \frac{2 \Gamma_{n}}{\Gamma_J} -1 \end{array} \right]$ (C.122)

The normalized scattering matrix can be expressed as a negative Householder reflection

$\displaystyle \tilde{\mathbf{A}}= \frac{2}{ \vert\vert\,\tilde{{\bm \Gamma}}\,\vert\vert ^2}\tilde{{\bm \Gamma}}\tilde{{\bm \Gamma}}^T-\mathbf{I}$ (C.123)

where $ \tilde{{\bm \Gamma}}^T= [\sqrt{\Gamma_1},\ldots,\sqrt{\Gamma_N}]$, and $ \Gamma_i$ is the wave admittance in the $ i$th waveguide branch. To eliminate the sign inversion, the reflections at the far end of each waveguide can be chosen as -1 instead of 1. The geometric interpretation of (C.124) is that the incoming pressure waves are reflected about the vector $ \tilde{{\bm \Gamma}}$. Unnormalized scattering junctions can be expressed in the form of an ``oblique'' Householder reflection $ \mathbf{A}= 2\mathbf{1}{\bm \Gamma}^T/\left<\mathbf{1},{{\bm \Gamma}}\right>-\mathbf{I}$, where $ \mathbf{1}^T=[1,\ldots,1]$ and $ {\bm \Gamma}^T= [\Gamma_1,\ldots,\Gamma_N]$.

General Conditions for Losslessness

The scattering matrices for lossless physical waveguide junctions give an apparently unexplored class of lossless FDN prototypes. However, this is just a subset of all possible lossless feedback matrices. We are therefore interested in the most general conditions for losslessness of an FDN feedback matrix. The results below are adapted from [463,385].

Consider the general case in which $ \mathbf{A}$ is allowed to be any scattering matrix, i.e., it is associated with a not-necessarily-physical junction of $ N$ physical waveguides. Following the definition of losslessness in classical network theory, we may say that a waveguide scattering matrix $ \mathbf{A}$ is said to be lossless if the total complex power [35] at the junction is scattering invariant, i.e.,

$\displaystyle {\mathbf{p}^+}^\ast {\bm \Gamma}\mathbf{p}^+$ $\displaystyle =$ $\displaystyle {\mathbf{p}^-}^\ast {\bm \Gamma}\mathbf{p}^-$  
$\displaystyle \implies \quad \mathbf{A}^\ast {\bm \Gamma}\mathbf{A}$ $\displaystyle =$ $\displaystyle {\bm \Gamma} \protect$ (C.124)

where $ {\bm \Gamma}$ is any Hermitian, positive-definite matrix (which has an interpretation as a generalized junction admittance). The form $ x^\ast {\bm \Gamma} x$ is by definition the square of the elliptic norm of $ x$ induced by $ {\bm \Gamma}$, or $ \vert\vert\,x\,\vert\vert _{\bm \Gamma}^2 = x^\ast {\bm \Gamma}x$. Setting $ {\bm \Gamma}=\mathbf{I}$, we obtain that $ \mathbf{A}$ must be unitary. This is the case commonly used in current FDN practice.

The following theorem gives a general characterization of lossless scattering:

Theorem: A scattering matrix (FDN feedback matrix) $ \mathbf{A}$ is lossless if and only if its eigenvalues lie on the unit circle and its eigenvectors are linearly independent.

Proof: Since $ {\bm \Gamma}$ is positive definite, it can be factored (by the Cholesky factorization) into the form $ {\bm \Gamma}= \mathbf{U}^\ast \mathbf{U}$, where $ \mathbf{U}$ is an upper triangular matrix, and $ \mathbf{U}^\ast $ denotes the Hermitian transpose of $ \mathbf{U}$, i.e., $ \mathbf{U}^\ast \isdef \overline{\mathbf{U}}^T$. Since $ {\bm \Gamma}$ is positive definite, $ \mathbf{U}$ is nonsingular and can be used as a similarity transformation matrix. Applying the Cholesky decomposition $ {\bm \Gamma}= \mathbf{U}^\ast \mathbf{U}$ in Eq.$ \,$(C.125) yields

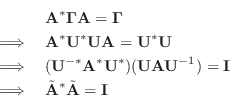
\begin{eqnarray*} & & \mathbf{A}^\ast {\bm \Gamma}\mathbf{A}= {\bm \Gamma}\\ &\... ...\implies& \tilde{\mathbf{A}}^\ast \tilde{\mathbf{A}}= \mathbf{I} \end{eqnarray*}

where $ \mathbf{U}^{-\ast}\isdef (\mathbf{U}^{-1})^\ast$, and

$\displaystyle \tilde{\mathbf{A}}\isdef \mathbf{U}\mathbf{A}\mathbf{U}^{-1} $

is similar to $ \mathbf{A}$ using $ \mathbf{U}^{-1}$ as the similarity transform matrix. Since $ \tilde{\mathbf{A}}$ is unitary, its eigenvalues have modulus 1. Hence, the eigenvalues of every lossless scattering matrix lie on the unit circle in the $ z$ plane. It readily follows from similarity to $ \tilde{\mathbf{A}}$ that $ \mathbf{A}$ admits $ N$ linearly independent eigenvectors. In fact, $ \tilde{\mathbf{A}}$ is a normal matrix ( $ \mathbf{A}\tilde{\mathbf{A}}= \tilde{\mathbf{A}}\mathbf{A}$), since every unitary matrix is normal, and normal matrices admit a basis of linearly independent eigenvectors [346].

Conversely, assume $ \vert\lambda\vert = 1$ for each eigenvalue of $ \mathbf{A}$, and that there exists a matrix $ \mathbf{E}$ of linearly independent eigenvectors of $ \mathbf{A}$. The matrix $ \mathbf{E}$ diagonalizes $ \mathbf{A}$ to give $ \mathbf{E}^{-1}\mathbf{A}\mathbf{E}= \mathbf{D}$, where $ \mathbf{D}=$   diag$ (\lambda_1,\dots,\lambda_N)$. Taking the Hermitian transform of this equation gives $ \mathbf{E}^\ast \mathbf{A}^\ast \mathbf{E}^{-\ast}= \mathbf{D}^\ast $. Multiplying, we obtain $ \mathbf{E}^\ast \mathbf{A}^\ast \mathbf{E}^{-\ast}\mathbf{E}^{-1}\mathbf{A}\ma... ...t \mathbf{E}^{-\ast}\mathbf{E}^{-1}\mathbf{A}=\mathbf{E}^{-\ast}\mathbf{E}^{-1}$. Thus, (C.125) is satisfied for $ {\bm \Gamma}=\mathbf{E}^{-\ast}\mathbf{E}^{-1}$ which is Hermitian and positive definite. $ \Box$

Thus, lossless scattering matrices may be fully parametrized as $ \mathbf{A} = \mathbf{E}^{-1}\mathbf{D}\mathbf{E}$, where $ \mathbf{D}$ is any unit-modulus diagonal matrix, and $ \mathbf{E}$ is any invertible matrix. In the real case, we have $ \mathbf{D}=$   diag$ (\pm 1)$ and $ \mathbf{E}\in\Re^{N\times N}$.

Note that not all lossless scattering matrices have a simple physical interpretation as a scattering matrix for an intersection of $ N$ lossless reflectively terminated waveguides. In addition to these cases (generated by all non-negative branch impedances), there are additional cases corresponding to sign flips and branch permutations at the junction. In terms of classical network theory [35], such additional cases can be seen as arising from the use of ``gyrators'' and/or ``circulators'' at the scattering junction [433]).

Next Section:
Waveguide Transformers and Gyrators
Previous Section:
Digital Waveguide Mesh