DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Relation to Finite Difference Approximation

The Finite Difference Approximation (FDA) (§7.3.1) is a special case of the matched $ z$ transformation applied to the point $ s=0$. To see this, simply set $ a=0$ in Eq.$ \,$(8.5) to obtain

$\displaystyle s \;\to\; 1 - z^{-1} \protect$ (9.7)

which is the FDA definition in the frequency domain given in Eq.$ \,$(7.3).

Since the FDA equals the match z transformation for the point $ s=0$, it maps analog dc ($ s=0$) to digital dc ($ z=1$) exactly. However, that is the only point on the frequency axis that is perfectly mapped, as shown in Fig.7.15.

State Space Approach to Modal Expansions

The preceding discussion of modal synthesis was based primarily on fitting a sum of biquads to measured frequency-response peaks. A more general way of arriving at a modal representation is to first form a state space model of the system [449], and then convert to the modal representation by diagonalizing the state-space model. This approach has the advantage of preserving system behavior between the given inputs and outputs. Specifically, the similarity transform used to diagonalize the system provides new input and output gain vectors which properly excite and observe the system modes precisely as in the original system. This procedure is especially more convenient than the transfer-function based approach above when there are multiple inputs and outputs. For some mathematical details, see [449]9.7For a related worked example, see §C.17.6.

Delay Loop Expansion

When a subset of the resonating modes are nearly harmonically tuned, it can be much more computationally efficient to use a filtered delay loop (see §2.6.5) to generate an entire quasi-harmonic series of modes rather than using a biquad for each modal peak [439]. In this case, the resonator model becomes

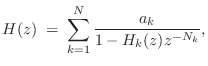
$\displaystyle H(z) \eqsp \sum_{k=1}^N \frac{a_k}{1 - H_k(z) z^{-N_k}}, $

where $ N_k$ is the length of the delay line in the $ k$th comb filter, and $ H_k(z)$ is a low-order filter which can be used to adjust finely the amplitudes and frequencies of the resonances of the $ k$th comb filter [428]. Recall (Chapter 6) that a single filtered delay loop efficiently models a distributed 1D propagation medium such as a vibrating string or acoustic tube. More abstractly, a superposition of such quasi-harmonic mode series can provide a computationally efficient psychoacoustic equivalent approximation to arbitrary collections of modes in the range of human hearing.

Note that when $ H_k(z)$ is close to $ -1$ instead of $ +1$, primarily only odd harmonic resonances are produced, as has been used in modeling the clarinet [431].

Next Section:
Ideal Differentiator (Spring Admittance)
Previous Section:
Further Reading in Nonlinear Methods