Free Books    Physical Audio Signal Processing  

Two-Port Series Adaptor for Force Waves

Figure F.6a illustrates a generic two-port description of the series adaptor.

Figure F.6: a) Two-port description of the adaptor implementing a series connection between reference impedances $ R_1$ and $ R_2$. b) Corresponding series force scattering junction (adaptor wave flow diagram) in Kelly-Lochbaum form.
\includegraphics[width=\twidth]{eps/lAdaptorSeries}

As discussed in §7.2, a series connection is characterized by a common velocity and forces which sum to zero at the junction:

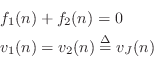
\begin{eqnarray*} && f_1(n) + f_2(n) = 0\\ && v_1(n) = v_2(n) \isdef v_J(n) \end{eqnarray*}

The derivation can proceed exactly as for the parallel junction in §F.2.1, but with force and velocity interchanged, i.e., $ f\leftrightarrow v$, and with impedance and admittance interchanged, i.e., $ R\leftrightarrow \Gamma $. In this way, we may take the dual of Eq.$ \,$(F.14) to get

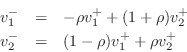
\begin{eqnarray*} v^{-}_1 &=& -\rho v^{+}_1 + (1+\rho) v^{+}_2\\ v^{-}_2 &=& (1-\rho)v^{+}_1 + \rho v^{+}_2 \end{eqnarray*}

diagrammed in Fig.F.7. Converting back to force wave variables via $ f^{{+}}_i=R_iv^{+}_i$ and $ f^{{-}}_i=-R_iv^{-}_i$, and noting that $ (1+\rho)R_1/R_2 = 1-\rho$, we obtain, finally,

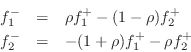
\begin{eqnarray*} f^{{-}}_1 &=& \rho f^{{+}}_1 - (1-\rho) f^{{+}}_2\\ f^{{-}}_2 &=& -(1+\rho)f^{{+}}_1 - \rho f^{{+}}_2 \end{eqnarray*}

as diagrammed in Fig.F.6b. The one-multiply form is now

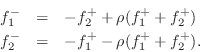
\begin{eqnarray*} f^{{-}}_1 &=& -f^{{+}}_2 + \rho(f^{{+}}_1 + f^{{+}}_2)\\ f^{{-}}_2 &=& -f^{{+}}_1 - \rho(f^{{+}}_1 + f^{{+}}_2). \end{eqnarray*}

Figure F.7: Series velocity scattering junction in Kelly-Lochbaum form.
\includegraphics[scale=0.9]{eps/lscat_vel_series_renum}

Next Section:
General Series Adaptor for Force Waves
Previous Section:
General Parallel Adaptor for Force Waves