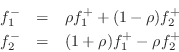DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Two-Port Parallel Adaptor for Force Waves

Figure F.5a illustrates a generic parallel two-port connection in terms of forces and velocities.

Figure: a) Two-port description of the adaptor implementing a parallel connection between reference impedances $ R_1$ and $ R_2$. b) Corresponding parallel force scattering junction (adaptor wave flow diagram) in Kelly-Lochbaum form. Compare with Fig.F.7.
\includegraphics[width=\twidth]{eps/lAdaptorParallel}

As discussed in §7.2, a parallel connection is characterized by a common force and velocities which sum to zero:

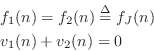
\begin{eqnarray*} && f_1(n) = f_2(n) \isdef f_J(n)\\ && v_1(n) + v_2(n) = 0 \end{eqnarray*}

Following the same derivation leading to Eq.$ \,$(F.2), and defining $ \Gamma _i=1/R_i$ for notational convenience, we obtain

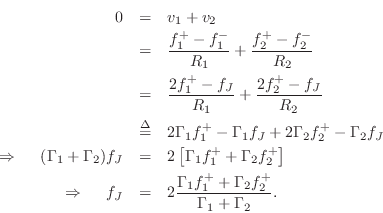
\begin{eqnarray*} 0 &=& v_1+v_2 \\ &=& \frac{f^{{+}}_1-f^{{-}}_1}{R_1} + \frac... ...amma _1 f^{{+}}_1 + \Gamma _2 f^{{+}}_2 }{\Gamma _1+\Gamma _2} . \end{eqnarray*}

The outgoing wave variables are given by

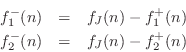
\begin{eqnarray*} f^{{-}}_1(n) &=& f_J(n) - f^{{+}}_1(n) \\ f^{{-}}_2(n) &=& f_J(n) - f^{{+}}_2(n) \end{eqnarray*}

Defining the reflection coefficient as

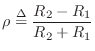
$\displaystyle \rho \isdef \frac{R_2-R_1}{R_2+R_1} $

we have that the scattering relations for the two-port parallel adaptor are

\begin{eqnarray*} f^{{-}}_1 &=& \rho f^{{+}}_1 + (1-\rho) f^{{+}}_2 \protect \\ f^{{-}}_2 &=& (1+\rho)f^{{+}}_1 - \rho f^{{+}}_2 \protect \end{eqnarray*}

as diagrammed in Fig.F.5b. This can be called the Kelly-Lochbaum implementation of the two-port force-wave adaptor.

Now that we have a proper scattering interface between two reference impedances, we may connect two wave digital elements together, setting $ R_1$ to the port impedance of element 1, and $ R_2$ to the port impedance of element 2. An example is shown in Fig.F.35.

The Kelly-Lochbaum adaptor in Fig.F.5b evidently requires four multiplies and two additions. Note that we can factor out the reflection coefficient in each equation to obtain

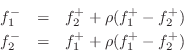
\begin{eqnarray*} f^{{-}}_1 &=& f^{{+}}_2 + \rho(f^{{+}}_1 - f^{{+}}_2)\\ f^{{-}}_2 &=& f^{{+}}_1 + \rho(f^{{+}}_1 - f^{{+}}_2) \end{eqnarray*}

which requires only one multiplication and three additions. This can be called the one-multiply form. The one-multiply form is most efficient in custom VLSI. The Kelly-Lochbaum form, on the other hand, may be more efficient in software, and slightly faster (by one addition) in parallel hardware.

Compatible Port Connections

Note carefully that to connect a wave digital element to port $ i$ of the adaptor, we route the signal $ f^{{-}}(n)$ coming out of the element to become $ f^{{+}}_i(n)$ on the adaptor port, and the signal $ f^{{-}}_i(n)$ coming out of port $ i$ of the adaptor goes into the element as $ f^{{+}}(n)$. Such a connection is said to be a compatible port connection. In other words, the connections must be made such that the arrows go in the same direction in the wave flow diagram.

Next Section:
General Parallel Adaptor for Force Waves
Previous Section:
Unit Elements