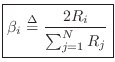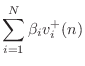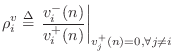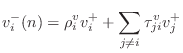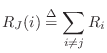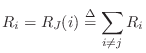DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

General Series Adaptor for Force Waves

In the more general case of $ N$ ports being connected in series, we have the physical constraints

\begin{eqnarray*} && v_1(n) = v_2(n) = \cdots = v_N(n) \isdef v_J(n)\\ && f_1(n) + f_2(n) + \cdots + f_N(n) = 0 \end{eqnarray*}

The derivation is the dual of that in the parallel case (cf. Eq.$ \,$(F.16)), i.e., force and velocity are interchanged, and impedance and admittance are interchanged:

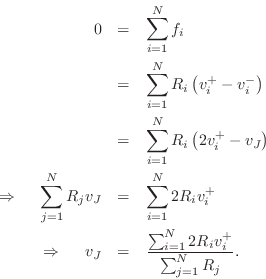
\begin{eqnarray*} 0 &=& \sum_{i=1}^N f_i \\ &=& \sum_{i=1}^NR_i\left(v^{+}_i-v... ...uad v_J &=& \frac{\sum_{i=1}^N 2R_i v^{+}_i}{\sum_{j=1}^N R_j} . \end{eqnarray*}

The outgoing wave variables are given by

$\displaystyle v^{-}_i(n) = v_J(n) - v^{+}_i(n) $

Beta Parameters

It is customary in the wave digital filter literature to define the beta parameters as

$\displaystyle \fbox{$\displaystyle \beta_i \isdef \frac{2R_i}{\sum_{j=1}^N R_j}$} \protect$ (F.26)

where $ R_i$ are the port impedances (attached element reference impedances). In terms of the beta parameters, the force-wave series adaptor performs the following computations:
$\displaystyle v_J(n)$ $\displaystyle =$ $\displaystyle \sum_{i=1}^N \beta_i v^{+}_i(n)\protect$ (F.27)
$\displaystyle v^{-}_i(n)$ $\displaystyle =$ $\displaystyle v_J(n) - v^{+}_i(n)\protect$ (F.28)

However, we normally employ a mixture of parallel and series adaptors, while keeping a force-wave simulation. Since $ f^{{+}}_i(n) = R_i v^{+}_i(n)$, we obtain, after a small amount of algebra, the following recipe for the series force-wave adaptor:

$\displaystyle f^{{+}}_J(n)$ $\displaystyle =$ $\displaystyle \sum_{i=1}^N f^{{+}}_i(n)\protect$ (F.29)
$\displaystyle f^{{-}}_i(n)$ $\displaystyle =$ $\displaystyle f^{{+}}_i(n) - \beta_if^{{+}}_J(n)\protect$ (F.30)

We see that we have $ N$ multiplies and $ 2N-1$ additions as in the parallel-adaptor case. However, we again have from Eq.$ \,$(F.26) that

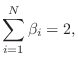
$\displaystyle \sum_{i=1}^N \beta_i = 2, $

so that we may implement one beta parameter as 2 minus the sum of the rest, thus eliminating a multiplication by creating a dependent port.

Reflection Coefficient, Series Case

The velocity reflection coefficient seen at port $ i$ is defined as

$\displaystyle \rho^v_i \isdef \left. \frac{v^{-}_i(n)}{v^{+}_i(n)} \right\vert _{v^{+}_j(n)=0, \forall j\neq i} \protect$ (F.31)

Representing the outgoing velocity wave $ v^{-}_i(n)$ as the superposition of the reflected wave $ \rho^v_iv^{+}_i(n)$ plus the $ N-1$ transmitted waves from the other ports, we have

$\displaystyle v^{-}_i(n) = \rho^v_i v^{+}_i + \sum_{j\neq i} \tau^v_{ji} v^{+}_j \protect$ (F.32)

where $ \tau^v_{ji}$ denotes the velocity transmission coefficientvelocity!transmission coefficient from port $ j$ to port $ i$. Substituting Eq.$ \,$(F.29) into Eq.$ \,$(F.30) yields

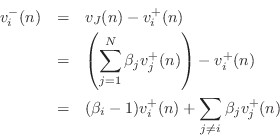
\begin{eqnarray*} v^{-}_i(n) &=& v_J(n) - v^{+}_i(n)\\ &=& \left(\sum_{j=1}^N ... ... &=& (\beta_i - 1)v^{+}_i(n) + \sum_{j\neq i} \beta_j v^{+}_j(n) \end{eqnarray*}

Equating like terms with Eq.$ \,$(F.32) gives

$\displaystyle \rho^v_i$ $\displaystyle =$ $\displaystyle \beta_i - 1 \protect$ (F.33)
$\displaystyle \tau^v_{ji}$ $\displaystyle =$ $\displaystyle \beta_j, \quad (i\neq j)$ (F.34)

Thus, the $ j$th beta parameter is the velocity transmission coefficient from $ j$th port to any other port (besides the $ i$th). To convert the transmission coefficient from the $ i$th port to the reflection coefficient for that port, we simply subtract 1. These relationships are specific to velocity waves at a series junction (cf. Eq.$ \,$(F.22)). They are exactly the dual of Equations (F.22-F.23) for force waves at a parallel junction.

Physical Derivation of Series Reflection Coefficient

Physically, the force-wave reflection coefficient seen at port $ i$ of a series adaptor is due to an impedance step from $ R_i$, that of the port interface, to a new impedance consisting of the series combination of all other port impedances meeting at the junction. Let

$\displaystyle R_J(i) \isdef \sum_{i\neq j} R_i \protect$ (F.35)

denote this series combination. Then we must have, as in Eq.$ \,$(F.25),

$\displaystyle \rho_i = \frac{R_J(i)-R_i}{R_J(i)+R_i}$ (F.36)

Let's check this ``physical'' derivation against the formal definition Eq.$ \,$(F.31) leading to $ \rho^v_i = \beta_i - 1$ in Eq.$ \,$(F.33). Define the total junction impedance as

$\displaystyle R_J \isdef \sum_{j=1}^N R_j $

This is the series combination of all impedances connected to the junction. Then by Eq.$ \,$(F.35), $ R_J = R_i + R_J(i)$ for all $ i$. From Eq.$ \,$(F.26), the velocity reflection coefficient is given by

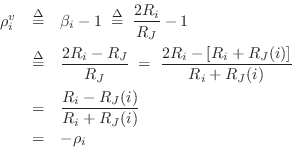
\begin{eqnarray*} \rho^v_i &\isdef & \beta_i - 1 \;\isdef \; \frac{2R_i}{R_J} -... ..._J(i)}\\ &=& \frac{R_i - R_J(i)}{R_i + R_J(i)}\\ &=& -\rho_i \end{eqnarray*}

Since

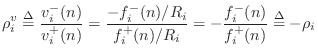
$\displaystyle \rho^v_i\isdef \frac{v^{-}_i(n)}{v^{+}_i(n)} = \frac{-f^{{-}}_i(n)/R_i}{f^{{+}}_i(n)/R_i} = - \frac{f^{{-}}_i(n)}{f^{{+}}_i(n)} \isdef -\rho_i $

the result follows.

Series Reflection Free Port

For port $ i$ to be reflection free in a series adaptor, we require

$\displaystyle R_i = R_J(i) \isdef \sum_{i\neq j} R_i \protect$ (F.37)

That is, the port's impedance must equal the series combination of the other port impedances at the junction. This result can be compared with that for the parallel junction in §F.2.2.

The series adaptor has now been derived in a way which emphasizes its duality with respect to the parallel adaptor.

Next Section:
``Piano hammer in flight''
Previous Section:
Two-Port Series Adaptor for Force Waves