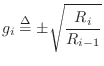Waveguide Transformers and Gyrators
The ideal transformer, depicted in Fig. C.37 a, is a
lossless two-port electric circuit element which scales up voltage by
a constant ![]() [110,35]. In other words, the voltage at
port 2 is always
[110,35]. In other words, the voltage at
port 2 is always ![]() times the voltage at port 1. Since power is
voltage times current, the current at port 2 must be
times the voltage at port 1. Since power is
voltage times current, the current at port 2 must be ![]() times the
current at port 1 in order for the transformer to be lossless. The
scaling constant
times the
current at port 1 in order for the transformer to be lossless. The
scaling constant ![]() is called the turns ratio because
transformers are built by coiling wire around two sides of a
magnetically permeable torus, and the number of winds around the port
2 side divided by the winding count on the port 1 side gives the
voltage stepping constant
is called the turns ratio because
transformers are built by coiling wire around two sides of a
magnetically permeable torus, and the number of winds around the port
2 side divided by the winding count on the port 1 side gives the
voltage stepping constant ![]() .
.
![\includegraphics[width=\twidth]{eps/lTransformer}](http://www.dsprelated.com/josimages_new/pasp/img4102.png) |
In the case of mechanical circuits, the two-port transformer relations appear as
![\begin{eqnarray*}
F_2(s) &=& g F_1(s) \\ [5pt]
V_2(s) &=& \frac{1}{g} V_1(s)
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img4103.png)
where ![]() and
and ![]() denote force and velocity, respectively.
We now convert these transformer describing
equations to the wave variable formulation. Let
denote force and velocity, respectively.
We now convert these transformer describing
equations to the wave variable formulation. Let ![]() and
and ![]() denote
the wave impedances on the port 1 and port 2 sides,
respectively, and define velocity as positive into the transformer. Then
denote
the wave impedances on the port 1 and port 2 sides,
respectively, and define velocity as positive into the transformer. Then
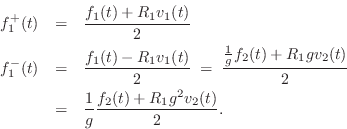
Similarly,
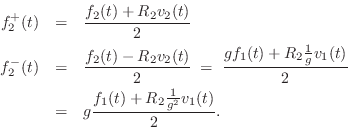
We see that choosing
![\begin{eqnarray*}
f^{{-}}_2(t) &=& g f^{{+}}_1(t)\\ [5pt]
f^{{-}}_1(t) &=& \frac{1}{g}f^{{+}}_2(t).
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img4107.png)
The corresponding wave flow diagram is shown in Fig. C.37 b.
Thus, a transformer with a voltage gain ![]() corresponds to simply
changing the wave impedance from
corresponds to simply
changing the wave impedance from ![]() to
to ![]() , where
, where
![]() . Note that the transformer implements a change
in wave impedance without scattering as occurs in physical
impedance steps (§C.8).
. Note that the transformer implements a change
in wave impedance without scattering as occurs in physical
impedance steps (§C.8).
Gyrators
Another way to define the ideal waveguide transformer is to ask for a
two-port element that joins two waveguide sections of differing wave
impedance in such a way that signal power is preserved and no
scattering occurs. From Ohm's Law for traveling waves
(Eq.![]() (6.6)), and from the definition of power waves
(§C.7.5), we see that to bridge an impedance
discontinuity between
(6.6)), and from the definition of power waves
(§C.7.5), we see that to bridge an impedance
discontinuity between ![]() and
and ![]() with no power change and no scattering requires the
relations
with no power change and no scattering requires the
relations
![$\displaystyle \frac{[f^{{+}}_i]^2}{R_i} = \frac{[f^{{+}}_{i-1}]^2}{R_{i-1}}, \qquad\qquad
\frac{[f^{{-}}_i]^2}{R_i} = \frac{[f^{{-}}_{i-1}]^2}{R_{i-1}}.
$](http://www.dsprelated.com/josimages_new/pasp/img4109.png)
where
Choosing the negative square root for
The dualizer is readily derived from Ohm's Law for traveling waves:
![\begin{eqnarray*}
f^{{+}}\eqsp Rv^{+}, \qquad
f^{{-}}\eqsp -Rv^{-}\\ [5pt]
\Lon...
...i\eqsp Rv^{+}_{i-1}, \qquad
v^{-}_{i-1} \eqsp -R^{-1} f^{{-}}_i
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img4112.png)
In this case, velocity waves in section ![]() are converted to force
waves in section
are converted to force
waves in section ![]() , and vice versa (all at wave impedance
, and vice versa (all at wave impedance ![]() ). The
wave impedance can be changed as well by cascading a transformer with
the dualizer, which changes
). The
wave impedance can be changed as well by cascading a transformer with
the dualizer, which changes ![]() to
to
![]() (where we assume
(where we assume ![]() ). Finally, the velocity waves in section
). Finally, the velocity waves in section
![]() can be scaled to equal their corresponding force waves by
introducing a transformer
can be scaled to equal their corresponding force waves by
introducing a transformer
![]() on the left, which then
coincides Eq.
on the left, which then
coincides Eq.![]() (C.126) (but with a minus sign in the second equation).
(C.126) (but with a minus sign in the second equation).
Next Section:
The Digital Waveguide Oscillator
Previous Section:
FDNs as Digital Waveguide Networks