DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

``Piano hammer in flight''

Suppose we wish to model a situation in which a mass of size $ m$ kilograms is traveling with a constant velocity. This is an appropriate model for a piano hammer after its key has been pressed and before the hammer has reached the string.

Figure F.2 shows the ``wave digital mass'' derived previously. The derivation consisted of inserting an infinitesimal waveguideF.3 having (real) impedance $ m$, solving for the force-wave reflectance of the mass as seen from the waveguide, and then mapping it to the discrete time domain using the bilinear transform.

We now need to attach the other end of the transmission line to a ``force source'' which applies a force of zero newtons to the mass. In other words, we need to terminate the line in a way that corresponds to zero force.

Let the force-wave components entering and leaving the mass be denoted $ f^{{+}}$ and $ f^{{-}}$, respectively (i.e., we are dropping the subscript `d' in Fig.F.2). The physical force associated with the mass is

$\displaystyle f(n) = f^{{+}}(n) + f^{{-}}(n) = f^{{+}}(n) - f^{{+}}(n-1) $

The zero-force case is therefore obtained when $ f^{{+}}(n) = -f^{{-}}(n) = f^{{+}}(n-1)$. This is illustrated in Fig.F.8.

Figure F.8: Wave digital mass in flight at a constant velocity.
\includegraphics{eps/wdhammer}

Figure F.8a (left portion) illustrates what we derived by physical reasoning, and as such, it is most appropriate as a physical model of the constant-velocity mass. However, for actual implementation, Fig.F.8b would be more typical in practice. This is because we can always negate the state variable $ x(n)$ if needed to convert it from $ f^{{+}}(n-1)$ to $ f^{{-}}(n)$. It is very common to see final simplifications like this to maximize efficiency.

Note that Fig.F.8b can be interpreted physically as a wave digital spring displaced by a constant force $ f(n) = 2x(n)$.

Extracting Physical Quantities

Since we are using a force-wave simulation, the state variable $ x(n)$ (delay element output) is in units of physical force (newtons). Specifically, $ x(n) = f^{{+}}(n-1)$. (The physical force is, of course, 0, while its traveling-wave components are not 0 unless the mass is at rest.) Using the fundamental relations relating traveling force and velocity waves

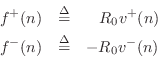
\begin{eqnarray*} f^{{+}}(n) &\isdef & \quad\! R_0 v^{+}(n)\\ f^{{-}}(n) &\isdef & - R_0 v^{-}(n)\\ \end{eqnarray*}

where $ R_0= m$ here, it is easy to convert the state variable $ x(n)$ to other physical units, as we now demonstrate.

The velocity of the mass, for example, is given by

$\displaystyle v(n) = v^{+}(n) + v^{-}(n) = \frac{f^{{+}}(n)}{m} - \frac{f^{{-}}(n)}{m} = \frac{2f^{{+}}(n)}{m} = \frac{2}{m}x(n) $

Thus, the state variable $ x(n)$ can be scaled by $ 2/m$ to ``read out'' the mass velocity.

The kinetic energy of the mass is given by

$\displaystyle {\cal E}_m = \frac{1}{2}mv^2(n) = \frac{2}{m}x^2(n) $

I.e., the square of the state variable $ x(n)$ can be scaled by $ 2/m$ to produce the physical kinetic energy associated with the mass.

Next Section:
Force Driving a Mass
Previous Section:
General Series Adaptor for Force Waves