Continuous-Time Fourier Theorems
Selected Fourier theorems for the continuous-time case are stated and proved in Appendix B. However, two are sufficiently important that we state them here.
Scaling Theorem
The scaling theorem (or similarity theorem) says that if
you horizontally ``stretch'' a signal by the factor ![]() in the
time domain, you ``squeeze'' and amplify its Fourier transform by the
same factor in the frequency domain. This is an important general
Fourier duality relationship:
in the
time domain, you ``squeeze'' and amplify its Fourier transform by the
same factor in the frequency domain. This is an important general
Fourier duality relationship:
Theorem: For all continuous-time functions ![]() possessing a Fourier
transform,
possessing a Fourier
transform,
where
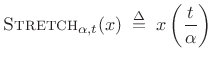
and
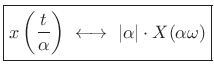 |
(3.41) |
Proof: See §B.4.
The scaling theorem is fundamentally restricted to the
continuous-time, continuous-frequency (Fourier transform) case. The
closest we come to the scaling theorem among the DTFT theorems
(§2.3) is the stretch (repeat) theorem
(page ![]() ). For this and other continuous-time Fourier
theorems, see Appendix B.
). For this and other continuous-time Fourier
theorems, see Appendix B.
Spectral Roll-Off
Definition: A function ![]() is said to be of order
is said to be of order
![]() if
there exist
if
there exist ![]() and some positive constant
and some positive constant ![]() such
that
such
that
![]() for all
for all
![]() .
.
Theorem: (Riemann Lemma):
If the derivatives up to order ![]() of a function
of a function ![]() exist and are
of bounded variation, then its Fourier Transform
exist and are
of bounded variation, then its Fourier Transform ![]() is
asymptotically of order
is
asymptotically of order
![]() , i.e.,
, i.e.,
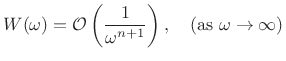 |
(3.42) |
Proof: See §B.18.
Next Section:
Spectral Interpolation
Previous Section:
Fourier Theorems for the DTFT



















