Spectral Interpolation
The need for spectral interpolation comes up in many situations. For example, we always use the DFT in practice, while conceptually we often prefer the DTFT. For time-limited signals, that is, signals which are zero outside some finite range, the DTFT can be computed from the DFT via spectral interpolation. Conversely, the DTFT of a time-limited signal can be sampled to obtain its DFT.3.7Another application of DFT interpolation is spectral peak estimation, which we take up in Chapter 5; in this situation, we start with a sampled spectral peak from a DFT, and we use interpolation to estimate the frequency of the peak more accurately than what we get by rounding to the nearest DFT bin frequency.
The following sections describe the theoretical and practical details of ideal spectral interpolation.
Ideal Spectral Interpolation
Ideally, the spectrum of any signal ![]() at any frequency
at any frequency
![]() is obtained by projecting the signal
is obtained by projecting the signal ![]() onto the
zero-phase, unit-amplitude, complex sinusoid at frequency
onto the
zero-phase, unit-amplitude, complex sinusoid at frequency ![]() [264]:
[264]:
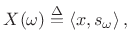 |
(3.43) |
where
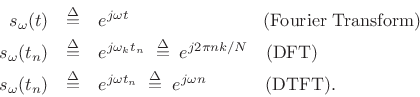
Thus, for signals in the DTFT domain which are time limited to
![]() ,
we obtain
,
we obtain
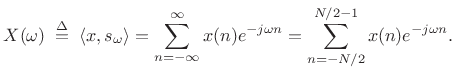 |
(3.44) |
This can be thought of as a zero-centered DFT evaluated at
Interpolating a DFT
Starting with a sampled spectrum
![]() ,
,
![]() ,
typically obtained from a DFT, we can interpolate by taking the DTFT
of the IDFT which is not periodically extended, but instead
zero-padded [264]:3.8
,
typically obtained from a DFT, we can interpolate by taking the DTFT
of the IDFT which is not periodically extended, but instead
zero-padded [264]:3.8
![\begin{eqnarray*}
X(\omega) &=& \hbox{\sc DTFT}(\hbox{\sc ZeroPad}_{\infty}(\hbox{\sc IDFT}_N(X)))\\
&\isdef & \sum_{n=-N/2}^{N/2-1}\left[\frac{1}{N}\sum_{k=0}^{N-1}X(\omega_k)
e^{j\omega_k n}\right]e^{-j\omega n}\\
&=& \sum_{k=0}^{N-1}X(\omega_k)
\left[\frac{1}{N}\sum_{n=-N/2}^{N/2-1} e^{j(\omega_k-\omega) n}\right]\\
&=& \sum_{k=0}^{N-1}X(\omega_k)\,\hbox{asinc}_N(\omega-\omega_k)\\
&=& \left<X,\hbox{\sc Sample}_N\{\hbox{\sc Shift}_{\omega}(\hbox{asinc}_N)\}\right>
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img261.png)
(The aliased sinc function,
![]() , is derived in
§3.1.)
Thus, zero-padding in the time domain interpolates a spectrum
consisting of
, is derived in
§3.1.)
Thus, zero-padding in the time domain interpolates a spectrum
consisting of ![]() samples around the unit circle by means of ``
samples around the unit circle by means of ``
![]() interpolation.'' This is ideal,
time-limited interpolation
in the frequency domain using the
aliased sinc function as an interpolation kernel. We can almost
rewrite the last line above as
interpolation.'' This is ideal,
time-limited interpolation
in the frequency domain using the
aliased sinc function as an interpolation kernel. We can almost
rewrite the last line above as
![]() ,
but such an expression would normally be defined only for
,
but such an expression would normally be defined only for
![]() , where
, where ![]() is some integer, since
is some integer, since ![]() is
discrete while
is
discrete while
![]() is continuous.
is continuous.
Figure F.1 lists a matlab function for performing ideal spectral interpolation directly in the frequency domain. Such an approach is normally only used when non-uniform sampling of the frequency axis is needed. For uniform spectral upsampling, it is more typical to take an inverse FFT, zero pad, then a longer FFT, as discussed further in the next section.
Zero Padding in the Time Domain
Unlike time-domain interpolation [270], ideal spectral interpolation is very easy to implement in practice by means of zero padding in the time domain. That is,
Since the frequency axis (the unit circle in the
Practical Zero Padding
To interpolate a uniformly sampled spectrum
![]() ,
,
![]() by the factor
by the factor ![]() , we may take the length
, we may take the length ![]() inverse DFT, append
inverse DFT, append
![]() zeros to the time-domain data, and take
a length
zeros to the time-domain data, and take
a length ![]() DFT. If
DFT. If ![]() is a power of two, then so is
is a power of two, then so is ![]() and
we can use a Cooley-Tukey FFT for both steps (which is very fast):
and
we can use a Cooley-Tukey FFT for both steps (which is very fast):
| (3.45) |
This operation creates
In matlab, we can specify zero-padding by simply providing the optional FFT-size argument:
X = fft(x,N); % FFT size N > length(x)
Zero-Padding to the Next Higher Power of 2
Another reason we zero-pad is to be able to use a Cooley-Tukey FFT with any
window length ![]() . When
. When ![]() is not a power of
is not a power of ![]() , we append enough
zeros to make the FFT size
, we append enough
zeros to make the FFT size ![]() be a power of
be a power of ![]() . In Matlab and
Octave, the function nextpow2 returns the next higher power
of 2 greater than or equal to its argument:
. In Matlab and
Octave, the function nextpow2 returns the next higher power
of 2 greater than or equal to its argument:
N = 2^nextpow2(M); % smallest M-compatible FFT size
Zero-Padding for Interpolating Spectral Displays
Suppose we perform spectrum analysis on some sinusoid using a length
![]() window. Without zero padding, the DFT length is
window. Without zero padding, the DFT length is ![]() . We may
regard the DFT as a critically sampled DTFT (sampled in
frequency). Since the bin separation in a length-
. We may
regard the DFT as a critically sampled DTFT (sampled in
frequency). Since the bin separation in a length-![]() DFT is
DFT is ![]() ,
and the zero-crossing interval for Blackman-Harris side lobes is
,
and the zero-crossing interval for Blackman-Harris side lobes is
![]() , we see that there is one bin per side lobe in the
sampled window transform. These spectral samples are illustrated for
a Hamming window transform in Fig.2.3b. Since
, we see that there is one bin per side lobe in the
sampled window transform. These spectral samples are illustrated for
a Hamming window transform in Fig.2.3b. Since ![]() in
Table 5.2, the main lobe is 4 samples wide when critically
sampled. The side lobes are one sample wide, and the samples happen
to hit near some of the side-lobe zero-crossings, which could be
misleading to the untrained eye if only the samples were shown. (Note
that the plot is clipped at -60 dB.)
in
Table 5.2, the main lobe is 4 samples wide when critically
sampled. The side lobes are one sample wide, and the samples happen
to hit near some of the side-lobe zero-crossings, which could be
misleading to the untrained eye if only the samples were shown. (Note
that the plot is clipped at -60 dB.)
![\includegraphics[width=\twidth]{eps/spectsamps}](http://www.dsprelated.com/josimages_new/sasp2/img279.png) |
If we now zero pad the Hamming-window by a factor of 2
(append 21 zeros to the length ![]() window and take an
window and take an ![]() point
DFT), we obtain the result shown in Fig.2.4. In this case,
the main lobe is 8 samples wide, and there are two samples per side
lobe. This is significantly better for display even though there is
no new information in the spectrum relative to Fig.2.3.3.10
point
DFT), we obtain the result shown in Fig.2.4. In this case,
the main lobe is 8 samples wide, and there are two samples per side
lobe. This is significantly better for display even though there is
no new information in the spectrum relative to Fig.2.3.3.10
Incidentally, the solid lines in Fig.2.3b and
2.4b indicating the ``true'' DTFT were computed
using a zero-padding factor of
![]() , and they were virtually
indistinguishable visually from
, and they were virtually
indistinguishable visually from ![]() . (
. (![]() is not enough.)
is not enough.)
![\includegraphics[width=\twidth]{eps/spectsamps2}](http://www.dsprelated.com/josimages_new/sasp2/img285.png) |
Zero-Padding for Interpolating Spectral Peaks
For sinusoidal peak-finding, spectral interpolation via zero-padding gets us closer to the true maximum of the main lobe when we simply take the maximum-magnitude FFT-bin as our estimate.
The examples in Fig.2.5 show how zero-padding helps in clarifying the true peak of the sampled window transform. With enough zero-padding, even very simple interpolation methods, such as quadratic polynomial interpolation, will give accurate peak estimates.
![\includegraphics[width=0.7\twidth]{eps/spectsamps3}](http://www.dsprelated.com/josimages_new/sasp2/img286.png) |
Another illustration of zero-padding appears in Section 8.1.3 of [264].
Zero-Phase Zero Padding
The previous zero-padding example used the causal Hamming window, and the appended zeros all went to the right of the window in the FFT input buffer (see Fig.2.4a). When using zero-phase FFT windows (usually the best choice), the zero-padding goes in the middle of the FFT buffer, as we now illustrate.
We look at zero-phase zero-padding using a Blackman window (§3.3.1) which has good, though suboptimal, characteristics for audio work.3.11
Figure 2.6a shows a windowed segment of some sinusoidal data,
with the window also shown as an envelope. Figure 2.6b shows
the same data loaded into an FFT input buffer with a factor of 2
zero-phase zero padding. Note that all time is ``modulo ![]() '' for a
length
'' for a
length ![]() FFT. As a result, negative times
FFT. As a result, negative times ![]() map to
map to ![]() in the
FFT input buffer.
in the
FFT input buffer.
![\includegraphics[width=\twidth]{eps/zpblackmanT}](http://www.dsprelated.com/josimages_new/sasp2/img289.png) |
Figure 2.7a shows the result of performing an FFT on the data
of Fig.2.6b. Since frequency indices are also modulo ![]() ,
the negative-frequency bins appear in the right half of the
buffer. Figure 2.6b shows the same data ``rotated'' so that
bin number is in order of physical frequency from
,
the negative-frequency bins appear in the right half of the
buffer. Figure 2.6b shows the same data ``rotated'' so that
bin number is in order of physical frequency from ![]() to
to ![]() .
If
.
If ![]() is the bin number, then the frequency in Hz is given by
is the bin number, then the frequency in Hz is given by ![]() , where
, where ![]() denotes the sampling rate and
denotes the sampling rate and ![]() is the FFT size.
is the FFT size.
![\includegraphics[width=\twidth]{eps/zpblackmanF}](http://www.dsprelated.com/josimages_new/sasp2/img293.png) |
The Matlab script for creating Figures 2.6 and 2.7 is listed in in §F.1.1.
Matlab/Octave fftshift utility
Matlab and Octave have a simple utility called fftshift that performs this bin rotation. Consider the following example:
octave:4> fftshift([1 2 3 4]) ans = 3 4 1 2 octave:5>If the vector [1 2 3 4] is the output of a length 4 FFT, then the first element (1) is the dc term, and the third element (3) is the point at half the sampling rate (
Another reasonable result would be fftshift([1 2 3 4]) == [4 1
2 3], which defines half the sampling rate as a positive frequency.
However, giving ![]() to the negative frequencies balances giving dc
to the positive frequencies, and the number of samples on both sides
is then the same. For an odd-length DFT, there is no point at
to the negative frequencies balances giving dc
to the positive frequencies, and the number of samples on both sides
is then the same. For an odd-length DFT, there is no point at
![]() , so the result
, so the result
octave:4> fftshift([1 2 3]) ans = 3 1 2 octave:5>is the only reasonable answer, corresponding to frequencies
Index Ranges for Zero-Phase Zero-Padding
Having looked at zero-phase zero-padding ``pictorially'' in matlab
buffers, let's now specify the index-ranges mathematically. Denote
the window length by ![]() (an odd integer) and the FFT length by
(an odd integer) and the FFT length by ![]() (a power of 2). Then the windowed data will occupy indices 0
to
(a power of 2). Then the windowed data will occupy indices 0
to
![]() (positive-time segment), and
(positive-time segment), and ![]() to
to ![]() (negative-time segment). Here we are assuming a 0-based indexing
scheme as used in C or C++. We add 1 to all indices for matlab
indexing to obtain 1:(M-1)/2+1 and N-(M-1)/2+1:N,
respectively. The zero-padding zeros go in between these ranges,
i.e., from
(negative-time segment). Here we are assuming a 0-based indexing
scheme as used in C or C++. We add 1 to all indices for matlab
indexing to obtain 1:(M-1)/2+1 and N-(M-1)/2+1:N,
respectively. The zero-padding zeros go in between these ranges,
i.e., from
![]() to
to
![]() .
.
Summary
To summarize, zero-padding is used for
- padding out to the next higher power of 2 so a Cooley-Tukey FFT can be used with any window length,
- improving the quality of spectral displays, and
- oversampling spectral peaks so that some simple final interpolation will be accurate.
Some examples of interpolated spectral display by means of zero-padding may be seen in §3.4.
Next Section:
The Rectangular Window
Previous Section:
Continuous-Time Fourier Theorems




















