Dolph-Chebyshev Window Theory
In this section, the main elements of the theory behind the Dolph-Chebyshev window are summarized.
Chebyshev Polynomials
The ![]() th Chebyshev polynomial may be defined by
th Chebyshev polynomial may be defined by
![$\displaystyle T_n(x) = \left\{\begin{array}{ll} \cos[n\cos^{-1}(x)], & \vert x\vert\le1 \\ [5pt] \cosh[n\cosh^{-1}(x)], & \vert x\vert>1 \\ \end{array} \right..$](http://www.dsprelated.com/josimages_new/sasp2/img534.png) |
(4.46) |
The first three even-order cases are plotted in Fig.3.35. (We will only need the even orders for making Chebyshev windows, as only they are symmetric about time 0.) Clearly,
| (4.47) |
for
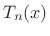 is an
is an  th-order polynomial in
th-order polynomial in  .
.
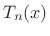 is an even function when
is an even function when  is an even integer,
and odd when
is an even integer,
and odd when  is odd.
is odd.
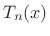 has
has  zeros in the open interval
zeros in the open interval 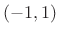 , and
, and
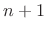 extrema in the closed interval
extrema in the closed interval ![$ [-1,1]$](http://www.dsprelated.com/josimages_new/sasp2/img543.png) .
.
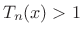 for
for 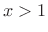 .
.
Dolph-Chebyshev Window Definition
Let ![]() denote the desired window length. Then the zero-phase
Dolph-Chebyshev window is defined in the frequency domain by
[155]
denote the desired window length. Then the zero-phase
Dolph-Chebyshev window is defined in the frequency domain by
[155]
![$\displaystyle W(\omega) = \frac{T_{M-1}[x_0 \cos(\omega/2)]}{T_{M-1}(x_0)}$](http://www.dsprelated.com/josimages_new/sasp2/img546.png) |
(4.48) |
where
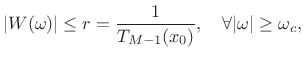 |
(4.49) |
where
![$\displaystyle \omega_c \isdefs 2\cos^{-1}\left[\frac{1}{x_0}\right].$](http://www.dsprelated.com/josimages_new/sasp2/img549.png) |
(4.50) |
Expanding
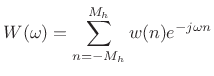 |
(4.51) |
where
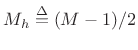 . Thus, the coefficients
. Thus, the coefficients
Dolph-Chebyshev Window Main-Lobe Width
Given the window length ![]() and ripple magnitude
and ripple magnitude ![]() , the main-lobe
width
, the main-lobe
width ![]() may be computed as follows [155]:
may be computed as follows [155]:
![\begin{eqnarray*}
x_0 &=& \cosh\left[\frac{\cosh^{-1}\left(\frac{1}{r}\right)}{M-1}\right]\\
\omega_c &=& 2\cos^{-1}\left(\frac{1}{x_0}\right)
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img553.png)
This is the smallest main-lobe width possible for the given window length and side-lobe spec.
Dolph-Chebyshev Window Length Computation
Given a prescribed side-lobe ripple-magnitude ![]() and main-lobe width
and main-lobe width
![]() , the required window length
, the required window length ![]() is given by [155]
is given by [155]
![$\displaystyle M = 1 + \frac{\cosh^{-1}(1/r)}{\cosh^{-1}[\sec(\omega_c/2)]}.$](http://www.dsprelated.com/josimages_new/sasp2/img554.png) |
(4.52) |
For
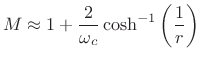 |
(4.53) |
Thus, half the time-bandwidth product in radians is approximately
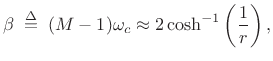 |
(4.54) |
where
Next Section:
Matlab for the Gaussian Window
Previous Section:
Chebyshev and Hamming Windows Compared








![\includegraphics[width=\twidth]{eps/first-even-chebs-c}](http://www.dsprelated.com/josimages_new/sasp2/img533.png)











