Dual of Constant Overlap-Add
In this section, we will derive the Fourier dual of the
Constant OverLap-Add (COLA) condition for STFT analysis windows
(discussed in §7.1). Recall that for perfect reconstruction
using a hop-size of ![]() samples, the window must be
samples, the window must be
![]() . We
will find that the equivalent frequency-domain condition is that the
window transform must have spectral zeros at all frequencies
which are a nonzero multiple of
. We
will find that the equivalent frequency-domain condition is that the
window transform must have spectral zeros at all frequencies
which are a nonzero multiple of ![]() . Following established
nomenclature for filter banks, we will say that such a window
transform is
. Following established
nomenclature for filter banks, we will say that such a window
transform is
![]() .
.
Poisson Summation Formula
Consider the summation of N complex sinusoids having frequencies uniformly spaced around the unit circle [264]:
![\begin{eqnarray*}
x(n) &\mathrel{\stackrel{\Delta}{=}}& \frac{1}{N} \sum_{k=0}^{N-1}e^{j\omega_kn} =
\left\{
\begin{array}{ll}
1 & n=0 \quad (\hbox{\sc mod}\ N) \\
0 & \mbox{elsewhere} \\
\end{array} \right. \\ [5pt]
&=& \hbox{\sc IDFT}_n(1 \cdots 1)
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img1454.png)
where
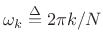 .
.
Setting ![]() (the FFT hop size) gives
(the FFT hop size) gives
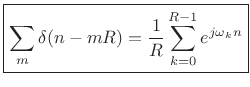 |
(9.26) |
where
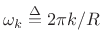 (harmonics of the frame rate).
(harmonics of the frame rate).
Let us now consider these equivalent signals as inputs to an LTI
system, with an impulse response given by ![]() , and frequency response
equal to
, and frequency response
equal to ![]() .
.
Looking across the top of Fig.8.16, for the case of input signal
![]() we have
we have
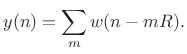 |
(9.27) |
Looking across the bottom of the figure, for the case of input signal
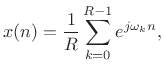 |
(9.28) |
we have the output signal
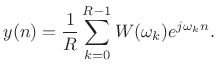 |
(9.29) |
This second form follows from the fact that complex sinusoids
Since the inputs were equal, the corresponding outputs must be equal too. This derives the Poisson Summation Formula (PSF):
Note that the PSF is the Fourier dual of the sampling theorem [270], [264, Appendix G].
The continuous-time PSF is derived in §B.15.
Frequency-Domain COLA Constraints
Recall that for error-free OLA processing, we required the constant-overlap-add (COLA) window constraint:
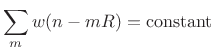 |
(9.31) |
Thanks to the PSF, we may now express the COLA constraint in the frequency domain:
| (9.32) |
In other terms,
Notation:
The ``Nyquist(
We may also refer to (8.33) as the ``weak COLA constraint'' in the frequency domain. It gives necessary and sufficient conditions for perfect reconstruction in overlap-add FFT processors. However, when the short-time spectrum is being modified, these conditions no longer apply, and a stronger COLA constraint is preferable.
Strong COLA
An overly strong (but sufficient) condition is to require that
the window transform ![]() be bandlimited consistent with
downsampling by
be bandlimited consistent with
downsampling by ![]() :
:
This condition is sufficient, but not necessary, for perfect OLA reconstruction. Strong COLA implies weak COLA, but it cannot be achieved exactly by finite-duration window functions.
When either of the strong or weak COLA conditions are met, we have
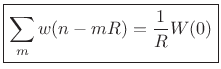 |
(9.34) |
That is, the overlap-add of the window
PSF Dual and Graphical Equalizers
Above, we used the Poisson Summation Formula to show that the constant-overlap-add of a window in the time domain is equivalent to the condition that the window transform have zero-crossings at all harmonics of the frame rate. In this section, we look briefly at the dual case: If the window transform is COLA in the frequency domain, what is the corresponding property of the window in the time domain? As one should expect, being COLA in the frequency domain corresponds to having specific uniform zero-crossings in the time domain.
Bandpass filters that sum to a constant provides an ideal basis for a graphic equalizer. In such a filter bank, when all the ``sliders'' of the equalizer are set to the same level, the filter bank reduces to no filtering at all, as desired.
Let ![]() denote the number of (complex) filters in our filter bank,
with pass-bands uniformly distributed around the unit circle. (We will
be using an FFT to implement such a filter bank.) Denote the
frequency response of the ``dc channel'' by
denote the number of (complex) filters in our filter bank,
with pass-bands uniformly distributed around the unit circle. (We will
be using an FFT to implement such a filter bank.) Denote the
frequency response of the ``dc channel'' by
![]() . Then the
constant overlap-add property of the
. Then the
constant overlap-add property of the ![]() -channel filter bank can be
expressed as
-channel filter bank can be
expressed as
| (9.35) |
which means
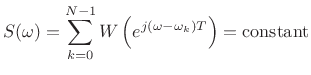 |
(9.36) |
where
 as usual. By the dual
of the Poisson summation formula, we have
as usual. By the dual
of the Poisson summation formula, we have
where
| (9.38) |
Thus, using the dual of the PSF, we have found that a good ![]() -channel
equalizer filter bank can be made using bandpass filters which have
zero-crossings at multiples of
-channel
equalizer filter bank can be made using bandpass filters which have
zero-crossings at multiples of ![]() samples, because that property
guarantees that the filter bank sums to a constant frequency response
when all channel gains are equal.
samples, because that property
guarantees that the filter bank sums to a constant frequency response
when all channel gains are equal.
The duality introduced in this section is the basis of the Filter-Bank Summation (FBS) interpretation of the short-time Fourier transform, and it is precisely the Fourier dual of the OverLap-Add (OLA) interpretation [9]. The FBS interpretation of the STFT is the subject of Chapter 9.
PSF and Weighted Overlap Add
Using ``square-root windows'' ![]() in the WOLA context, the
valid hop sizes
in the WOLA context, the
valid hop sizes ![]() are identical to those for
are identical to those for ![]() in the OLA case.
More generally, given any window
in the OLA case.
More generally, given any window ![]() for use in a WOLA system, it
is of interest to determine the hop sizes which yield perfect
reconstruction.
for use in a WOLA system, it
is of interest to determine the hop sizes which yield perfect
reconstruction.
Recall that, by the Poisson Summation Formula (PSF),
![$\displaystyle \zbox {\underbrace{\sum_m w(n-mR)}_{\hbox{\sc Alias}_R(w)} = \underbrace{\frac{1}{R}\sum_{k=0}^{R-1} W(\omega_k)e^{j\omega_k n}}_{\hbox{\sc DFT}_R^{-1} \left[\hbox{\sc Sample}_{\frac{2\pi}{R}}(W)\right]}} \quad \omega_k \isdef \frac{2\pi k}{R} \protect$](http://www.dsprelated.com/josimages_new/sasp2/img1466.png) |
(9.39) |
For WOLA, this is easily modified to become
![$\displaystyle \zbox {\underbrace{\sum_m w(n-mR)f(n-mR)}_{\hbox{\sc Alias}_R(w\cdot f)} = \underbrace{\frac{1}{R}\sum_{k=0}^{R-1} (W\ast F)(\omega_k)e^{j\omega_k n}}_{\hbox{\sc DFT}_R^{-1} \left[\hbox{\sc Sample}_{\frac{2\pi}{R}}(W\ast F)\right]}} \quad \omega_k \isdef \frac{2\pi k}{R}$](http://www.dsprelated.com/josimages_new/sasp2/img1482.png) |
(9.40) |
where
When ![]() , this becomes
, this becomes
![$\displaystyle \underbrace{\sum_m w^2(n-mR)}_{\hbox{\sc Alias}_R(w^2)} = \underbrace{\frac{1}{R}\sum_{k=0}^{R-1} (W\ast W)(\omega_k)e^{j\omega_k n}}_{\hbox{\sc DFT}_R^{-1} \left[\hbox{\sc Sample}_{\frac{2\pi}{R}}(W\ast W)\right]}, \quad \omega_k \isdef \frac{2\pi k}{R}$](http://www.dsprelated.com/josimages_new/sasp2/img1485.png) |
(9.41) |
Example COLA Windows for WOLA
In a weighted overlap-add system, the following windows can be used to satisfy the constant-overlap-add condition:
- For the rectangular window,
 , and
, and
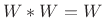 (since
(since
 is a sinc function which reduces to
is a sinc function which reduces to
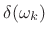 when
when
 , and
, and
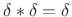 .
.
- For the Hamming window, the critically sampled window transform
has three nonzero samples (where the rectangular-window transform has
one). Therefore,
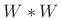 has
has 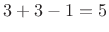 nonzero samples at critical
sampling. Measuring main-lobe width from zero-crossing to
zero-crossing as usual, we get
nonzero samples at critical
sampling. Measuring main-lobe width from zero-crossing to
zero-crossing as usual, we get
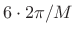 radians per sample, or
``6 side lobes'', for the width of
radians per sample, or
``6 side lobes'', for the width of 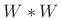 .
.
- The squared-Blackman window transform width is
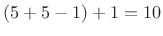 .
.
- The square of a length

 -term Blackman-Harris-family window
(where rect is
-term Blackman-Harris-family window
(where rect is 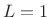 , Hann is
, Hann is 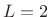 , etc.) has a main lobe of width
, etc.) has a main lobe of width
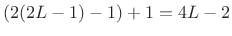 , measured from zero-crossing to zero-crossing in
``side-lobe units'' (
, measured from zero-crossing to zero-crossing in
``side-lobe units'' (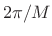 ). This is up from
). This is up from
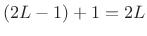 for the
original
for the
original  -term window.
-term window.
- The width of the main lobe can be used to determine the
hop size in the STFT, as will be discussed further in
Chapter 9.
Note that we need only find the first zero-crossing in the
window transform for any member of the Blackman-Harris window family
(Chapter 3), since nulls at all harmonics of
that frequency will always be present (at multiples of ![]() ).
).
Next Section:
Overlap-Save Method
Previous Section:
Convolving with Long Signals








![\begin{psfrags}
% latex2html id marker 22700\psfrag{d(n)}{\normalsize $\displaystyle\normalsize \sum_l\delta(n-lN)$\ }\psfrag{\makebox[0pt][l]{2}N}{\normalsize $-2N$}\psfrag{\makebox[0pt][l]{N}}{\normalsize $-N$}\psfrag{0}{\normalsize $0$}\psfrag{N}{\normalsize $N$}\psfrag{n}{\normalsize $n$}\psfrag{2N}{\normalsize $2N$}\psfrag{1}{\normalsize $1$}\begin{figure}[htbp]
\includegraphics[width=3.5in]{eps/delta}
\caption{Discrete-time impulse train created
by a sum of sampled complex sinusoids.}
\end{figure}
\end{psfrags}](http://www.dsprelated.com/josimages_new/sasp2/img1456.png)
![\begin{psfrags}
% latex2html id marker 22729\psfrag{w(n)}{\normalsize $w(n)$\ }\psfrag{W(w)}{\normalsize $W(\omega)$\ }\psfrag{timesum}{\normalsize $\displaystyle\sum_l\delta(n-lR)$\ }\psfrag{freqsum}{\normalsize $\frac{1}{R}\displaystyle\sum_k e^{j\omega_kn}$\ }\psfrag{t}{\normalsize $\displaystyle\sum_l w(n-lR)$\ }\psfrag{f}{\normalsize $\frac{1}{R}\displaystyle\sum_k W(\omega_k)e^{j\omega_kn}$\ }\psfrag{time}{\normalsize Time}\psfrag{freq}{\normalsize Frequency}\begin{figure}[htbp]
\includegraphics[width=4in]{eps/poisson}
\caption{Linear systems theory proof of the Poisson summation formula.}
\end{figure}
\end{psfrags}](http://www.dsprelated.com/josimages_new/sasp2/img1460.png)












