Frequency Modulation (FM) Synthesis
The first commercial digital sound synthesis method was Frequency Modulation (FM) synthesis [38,41,39], invented by John Chowning, the founding director of CCRMA. FM synthesis was discovered and initially developed in the 1970s [38]. The technology was commercialized by Yamaha Corporation, resulting in the DX-7 (1983), the first commercial digital music synthesizer, and the OPL chipset, initially in the SoundBlaster PC sound card, and later a standard chipset required for ``SoundBlaster compatibility'' in computer multimedia support. The original pioneer patent expired in 1996, but additional patents were filed later. It is said that this technology lives on in cell-phone ring-tone synthesis.
As discussed more fully in [264, p. 44], the formula for elementary FM synthesis is given by
where An example computer-music-style diagram is shown in Fig.G.6. Since the instantaneous frequency of a sinusoid is simply the time-derivative of its instantaneous phase, FM can also be regarded as phase modulation (PM). It is highly remarkable that such a simple algorithm can generate such a rich variety of musically useful sounds. This is probably best understood by thinking of FM as a spectral modeling technique, as will be illustrated further below.
FM Harmonic Amplitudes (Bessel Functions)
FM bandwidth expands as the modulation-amplitude ![]() is increased
in (G.2) above. The
is increased
in (G.2) above. The ![]() th harmonic amplitude is proportional to
the
th harmonic amplitude is proportional to
the ![]() th-order Bessel function of the first kind
th-order Bessel function of the first kind ![]() , evaluated at
the
FM modulation index
, evaluated at
the
FM modulation index
![]() . Figure G.7 illustrates
the behavior of
. Figure G.7 illustrates
the behavior of
![]() : As
: As ![]() is increased, more power
appears in the sidebands, at the expense of the fundamental. Thus,
increasing the FM index brightens the tone.
is increased, more power
appears in the sidebands, at the expense of the fundamental. Thus,
increasing the FM index brightens the tone.
![\includegraphics[width=\twidth]{eps/bessel}](http://www.dsprelated.com/josimages_new/sasp2/img2992.png) |
FM Brass
Jean-Claude Risset observed (1964-1969), based on spectrum analysis of brass tones [233], that the bandwidth of a brass instrument tone was roughly proportional to its overall amplitude. In other words, the spectrum brightened with amplitude. This observation inspired John Chowning's FM brass synthesis technique (starting in 1970[40]). For FM brass, the FM index is made proportional to carrier amplitude, thus yielding a dynamic brightness variation with amplitude that sounds consistently ``brassy''. A simple example of an FM brass instrument is shown in Fig.G.6 above. Note how the FM index is proportional to the amplitude envelope (carrier amplitude).
FM Voice
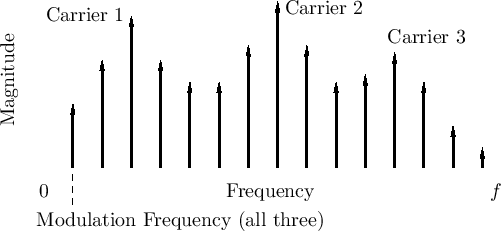
FM voice synthesis [39] can be viewed as compressed modeling of spectral formants. Figure G.8 shows the general idea. This kind of spectral approximation was used by John Chowning and others at CCRMA in the 1980s and beyond to develop convincing voices using FM. Another nice example was the FM piano developed by John Chowning and David Bristow [41].
A basic
FM operator,
consisting of two sinusoidal oscillators
(a ``modulator'' and a ``carrier'' oscillator, as written
in Eq.![]() (G.2)), can synthesize a useful approximation to
a formant group in a harmonic line spectrum. In this
technique, the carrier frequency is set near the formant center
frequency, rounded to the nearest harmonic frequency, and the
modulating frequency is set to the desired pitch (e.g., of a sung
voice [39]). The modulation index is set to give the
desired bandwidth for the formant group. For the singing
voice, three or more formant groups yields a
sung vowel sound. Thus, a sung vowel can be synthesized using
only six sinusoidal oscillators using FM. In straight additive
synthesis, a bound on the number of oscillators needed is given by the
upper band-limit divided by the fundamental frequency, which could be,
for a strongly projecting deep male voice, on the order of
(G.2)), can synthesize a useful approximation to
a formant group in a harmonic line spectrum. In this
technique, the carrier frequency is set near the formant center
frequency, rounded to the nearest harmonic frequency, and the
modulating frequency is set to the desired pitch (e.g., of a sung
voice [39]). The modulation index is set to give the
desired bandwidth for the formant group. For the singing
voice, three or more formant groups yields a
sung vowel sound. Thus, a sung vowel can be synthesized using
only six sinusoidal oscillators using FM. In straight additive
synthesis, a bound on the number of oscillators needed is given by the
upper band-limit divided by the fundamental frequency, which could be,
for a strongly projecting deep male voice, on the order of ![]() kHz
divided by 100 Hz, or 200 oscillators.
kHz
divided by 100 Hz, or 200 oscillators.
Today, FM synthesis is still a powerful spectral modeling technique in which ``formant harmonic groups'' are approximated by the spectrum of an elementary FM oscillator pair. This remains a valuable tool in environments where memory access is limited, such as in VLSI chips used in hand-held devices, as it requires less memory than wavetable synthesis (§G.8.4).
In the context of audio coding, FM synthesis can be considered a ``lossy compression method'' for additive synthesis.
Further Reading about FM Synthesis
For further reading about FM synthesis, see the original Chowning paper [38], paper anthologies including FM [236,234], or just about any computer-music text [235,183,60,216].
Next Section:
Phase Vocoder Sinusoidal Modeling
Previous Section:
Additive Synthesis