Perfect Reconstruction Filter Banks

Free Books Spectral Audio Signal Processing

We now consider filter banks with an arbitrary number of channels, and ask under what conditions do we obtain a perfect reconstruction filter bank? Polyphase analysis will give us the answer readily. Let's begin with the -channel filter bank in Fig.11.20. The downsampling factor is $R\leq N$ . For critical sampling, we set .

**Figure:** -channel filter bank.
$\includegraphics[width=\twidth]{eps/FBNchan}$

The next step is to expand each analysis filter into its -channel ``type I'' polyphase representation:

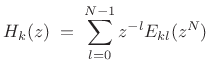$\displaystyle H_k(z) \eqsp \sum_{l=0}^{N-1} z^{-l} E_{kl}(z^N)$

(12.49)

$\displaystyle \underbrace{\left[\begin{array}{c} H_0(z) \\ [2pt] H_1(z) \\ [2pt] \vdots \\ [2pt] \!\!H_{N-1}(z)\!\!\end{array}\right]}_{\bold{h}(z)} = \underbrace{\left[\begin{array}{cccc} E_{0,0}(z^N) & E_{0,1}(z^N) & \cdots & E_{0,N-1}(z^N) \\ E_{1,0}(z^N) & E_{1,1}(z^N) & \cdots & E_{1,N-1}(z^N)\\ \vdots & \vdots & \cdots & \vdots\\ \!\!E_{N-1,0}(z^N) & E_{N-1,1}(z^N) & \cdots & E_{N-1,N-1}(z^N) \!\! \end{array}\right]}_{\bold{E}(z^N)} \underbrace{\left[\begin{array}{c} 1 \\ [2pt] z^{-1} \\ [2pt] \vdots \\ [2pt] \!\!z^{-(N-1)}\!\!\end{array}\right]}_{\bold{e}(z)}$

(12.50)

which we can write as

$\displaystyle \bold{h}(z) \eqsp \bold{E}(z^N)\bold{e}(z).$

(12.51)

Similarly, expand the synthesis filters in a type II polyphase decomposition:

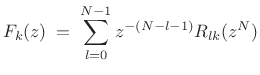$\displaystyle F_k(z) \eqsp \sum_{l=0}^{N-1} z^{-(N-l-1)}R_{lk}(z^N)$

(12.52)

$\displaystyle \underbrace{\left[\begin{array}{c} F_0(z) \\ [2pt] F_1(z) \\ [2pt] \vdots \\ [2pt] \!\!F_{N-1}(z)\!\!\end{array}\right]^T}_{\bold{f}^T(z)} \eqsp \underbrace{\left[\begin{array}{c} \!\!z^{-(N-1)}\!\! \\ [2pt] \!\!z^{-(N-2)}\!\! \\ [2pt] \vdots \\ [2pt] 1\end{array}\right]^T}_{{\tilde{\bold{e}}}(z)} \underbrace{\left[\begin{array}{cccc} R_{0,0}(z^N) & R_{0,1}(z^N) & \cdots & R_{0,N-1}(z^N) \\ R_{1,0}(z^N) & R_{1,1}(z^N) & \cdots & R_{1,N-1}(z^N)\\ \vdots & \vdots & \cdots & \vdots\\ \!\!R_{N-1,0}(z^N) & R_{N-1,1}(z^N) & \cdots & R_{N-1,N-1}(z^N)\!\! \end{array}\right]}_{\bold{R}(z^N)}$

(12.53)

which we can write as

$\displaystyle \bold{f}^T(z) \eqsp {\tilde{\bold{e}}}(z)\bold{R}(z^N).$

(12.54)

The polyphase representation can now be depicted as shown in Fig.11.21. When , commuting the up/downsamplers gives the result shown in Fig.11.22. We call $\bold{E}(z)$ the polyphase matrix.

**Figure:** Polyphase representation of the -channel filter bank.
$\includegraphics[width=\twidth]{eps/polyNchan}$

**Figure:** Efficient polyphase form of the -channel filter bank.
$\includegraphics[width=\twidth]{eps/polyNchanfast}$

As we will show below, the above simplification can be carried out more generally whenever divides (e.g., $R=N/2, N/3,\ldots, 1$ ). In these cases $\bold{E}(z)$ becomes $\bold{E}(z^{N/R})$ and $\bold{R}(z)$ becomes $\bold{R}(z^{N/R})$ .

Simple Examples of Perfect Reconstruction

If we can arrange to have

$\displaystyle \zbox {\bold{R}(z)\bold{E}(z) = \bold{I}_N}$

(12.55)

then the filter bank will reduce to the simple system shown in Fig.11.23.

**Figure:** Simplified filter bank when inverts .
$\includegraphics{eps/polyNchanI}$

Thus, when and $\bold{R}(z)\bold{E}(z)=\bold{I}_N$ , we have a simple parallelizer/serializer, which is perfect-reconstruction by inspection: Referring to Fig.11.23, think of the input samples as ``filling'' a length delay line over sample clocks. At time 0 , the downsamplers and upsamplers ``fire'', transferring (and zeros) from the delay line to the output delay chain, summing with zeros. Over the next clocks, makes its way toward the output, and zeros fill in behind it in the output delay chain. Simultaneously, the input buffer is being filled with samples of . At time , makes it to the output. At time , the downsamplers ``fire'' again, transferring a length ``buffer'' [ : ] to the upsamplers. On the same clock pulse, the upsamplers also ``fire'', transferring samples to the output delay chain. The bottom-most sample [ ] goes out immediately at time . Over the next sample clocks, the length output buffer will be ``drained'' and refilled by zeros. Simultaneously, the input buffer will be replaced by new samples of . At time , the downsamplers and upsamplers ``fire'', and the process goes on, repeating with period . The output of the -way parallelizer/serializer is therefore

$\displaystyle {\hat x}(n) \eqsp x(n-N+1)$

(12.56)

and we have perfect reconstruction.

Sliding Polyphase Filter Bank

**Figure:** Simplified filter bank when inverts and there are no downsamplers or upsamplers ( ).
$\includegraphics{eps/polyNchanIR1}$

When , there is no downsampling or upsampling, and the system further reduces to the case shown in Fig.11.24. Working backward along the output delay chain, the output sum can be written as

$\begin{eqnarray*} \hat{X}(z) &=& \left[z^{-0}z^{-(N-1)} + z^{-1}z^{-(N-2)} + z^{-2}z^{-(N-3)} + \cdots \right.\\ & & \left. + z^{-(N-2)}z^{-1} + z^{-(N-1)}z^{-0} \right] X(z)\\ &=& N z^{-(N-1)} X(z). \end{eqnarray*}$

Thus, when , the output is

$\displaystyle {\hat x}(n) \eqsp N x(n-N+1)$

(12.57)

and we again have perfect reconstruction.

Hopping Polyphase Filter Bank

When and divides , we have, by a similar analysis,

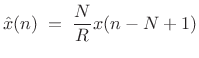$\displaystyle {\hat x}(n) \eqsp \frac{N}{R} x(n-N+1)$

(12.58)

which is again perfect reconstruction. Note the built-in overlap-add when .

Sufficient Condition for Perfect Reconstruction

Above, we found that, for any integer $1\leq R\leq N$ which divides , a sufficient condition for perfect reconstruction is

$\displaystyle \bold{P}(z)\isdefs \bold{R}(z)\bold{E}(z) \eqsp \bold{I}_N$

(12.59)

and the output signal is then

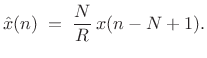$\displaystyle {\hat x}(n) \eqsp \frac{N}{R} \, x(n-N+1).$

(12.60)

More generally, we allow any nonzero scaling and any additional delay:

$\displaystyle \bold{P}(z) \eqsp \bold{R}(z)\bold{E}(z) \eqsp c\, z^{-K}\, \bold{I}_N \protect$

(12.61)

where $c\neq 0$ is any constant and is any nonnegative integer. In this case, the output signal is

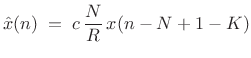$\displaystyle {\hat x}(n) \eqsp c\,\frac{N}{R} \, x(n-N+1-K)$

(12.62)

Thus, given any polyphase matrix $\bold{E}(z)$ , we can attempt to compute $\bold{R}(z) = \bold{E}^{-1}(z)$ : If it is stable, we can use it to build a perfect-reconstruction filter bank. However, if $\bold{E}(z)$ is FIR, $\bold{R}(z)$ will typically be IIR. In §11.5 below, we will look at paraunitary filter banks, for which $\bold{R}(z)$ is FIR and paraunitary whenever $\bold{E}(z)$ is.

Necessary and Sufficient Conditions for Perfect Reconstruction

It can be shown [287] that the most general conditions for perfect reconstruction are that

$\displaystyle \zbox {\bold{R}(z)\bold{E}(z) \eqsp c z^{-K} \left[\begin{array}{cc} \bold{0}_{(N-L)\times L} & z^{-1}\bold{I}_{N-L} \\ [2pt] \bold{I}_L & \bold{0}_{L \times (N-L)} \end{array}\right]}$

(12.63)

for some constant and some integer $K\geq 0$ , where is any integer between 0 and .

Note that the more general form of $\bold{R}(z)\bold{E}(z)$ above can be regarded as a (non-unique) square root of a vector unit delay, since

$\displaystyle \left[\begin{array}{cc} \bold{0}_{(N-L)\times L} & z^{-1}\bold{I}_{N-L} \\ [2pt] \bold{I}_L & \bold{0}_{L \times (N-L)} \end{array}\right]^2 \eqsp z^{-1}\bold{I}_N.$

(12.64)

Thus, the general case is the same thing as

$\displaystyle \bold{R}(z)\bold{E}(z) \eqsp c z^{-K} \bold{I}_N.$

(12.65)

except for some channel swapping and an extra sample of delay in some channels.

Polyphase View of the STFT

As a familiar special case, set

$\displaystyle \bold{E}(z) \eqsp \bold{W}_N^\ast$

(12.66)

where $\bold{W}_N^\ast$ is the DFT matrix:

$\displaystyle \bold{W}_N^\ast[kn] \eqsp \left[e^{-j2\pi kn/N}\right]$

(12.67)

The inverse of this polyphase matrix is then simply the inverse DFT matrix:

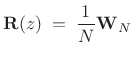$\displaystyle \bold{R}(z) \eqsp \frac{1}{N}\bold{W}_N$

(12.68)

Thus, the STFT (with rectangular window) is the simple special case of a perfect reconstruction filter bank for which the polyphase matrix is constant. It is also unitary; therefore, the STFT is an orthogonal filter bank.

The channel analysis and synthesis filters are, respectively,

$\begin{eqnarray*} H_k(z) &=& H_0(zW_N^k)\\ [5pt] F_k(z) &=& F_0(zW_N^{-k}) \end{eqnarray*}$

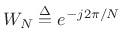where $W_N\isdef e^{-j2\pi/N}$ , and

$\displaystyle F_0(z)\eqsp H_0(z)\eqsp \sum_{n=0}^{N-1}z^{-n}\;\longleftrightarrow\;[1,1,\ldots,1]$

(12.69)

corresponding to the rectangular window.

**Figure 11.25:** Polyphase representation of the STFT with a rectangular window.
$\includegraphics[width=\twidth]{eps/polyNchanSTFT}$

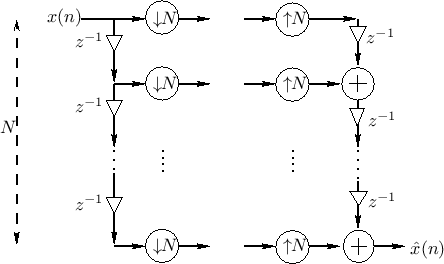
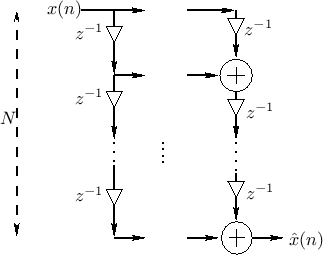
Looking again at the polyphase representation of the -channel filter bank with hop size , $\bold{E}(z)=\bold{W}_N^\ast$ , $\bold{R}(z)=\bold{W}_N$ , dividing , we have the system shown in Fig.11.25. Following the same analysis as in §11.4.1 leads to the following conclusion:

$\displaystyle \zbox {\hbox{The polyphase representation is an \emph{overlap-add} representation.}}$

Our analysis showed that the STFT using a rectangular window is a perfect reconstruction filter bank for all integer hop sizes in the set $R\in\{N,N/2,N/3,\ldots,N/N\}$ . The same type of analysis can be applied to the STFT using the other windows we've studied, including Portnoff windows.

Example: Polyphase Analysis of the STFT with 50% Overlap, Zero-Padding, and a Non-Rectangular Window

**Figure:** Polyphase representation of the STFT with a more general window and hop size ( % overlap).
$\includegraphics[width=\twidth]{eps/polyNchanWinZPSTFT}$

Figure 11.26 illustrates how a window and a hop size other than can be introduced into the polyphase representation of the STFT. The constant-overlap-add of the window is implemented in the synthesis delay chain (which is technically the transpose of a tapped delay line). The downsampling factor and window must be selected together to give constant overlap-add, independent of the choice of polyphase matrices $\bold{E}(z)$ and $\bold{R}(z)$ (shown here as the $\hbox{\sc DFT}$ and $\hbox{\sc IDFT}$ ).

Example: Polyphase Analysis of the Weighted Overlap Add Case: 50% Overlap, Zero-Padding, and a Non-Rectangular Window

We may convert the previous example to a weighted overlap-add (WOLA) (§8.6) filter bank by replacing each by $\sqrt{w(m)}$ and introducing these gains also between the $\hbox{\sc IDFT}$ and upsamplers, as shown in Fig.11.27.