Free Books
   Free Books    Spectral Audio Signal Processing  

Properly Anti-Aliasing Window Transforms

For simplicity, define window-transform bandlimits at first zero-crossings about the main lobe. Given the first zero of $ W(\omega)$ at $ L \frac{2\pi}{M} \leq \frac{\pi}{R}$ , we obtain

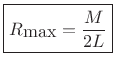$\displaystyle \zbox {R_{\hbox{max}}= \frac{M}{2L}}$ (10.27)

The following table gives maximum hop sizes for various window types in the Blackman-Harris family, where $ L$ is both the number of constant-plus-cosine terms in the window definition (§3.3) and the half-main-lobe width in units of side-lobe widths $ 2\pi/M$ . Also shown in the table is the maximum COLA hop size we determined in Chapter 8.
L Window Type (Length $ M$ ) $ R_{\hbox{max}}$ $ R_{\hbox{\hbox{\sc Cola}}}$
1 Rectangular M/2 M
2 Generalized Hamming M/4 M/2
3 Blackman Family M/6 M/3
L $ L$ -term Blackman-Harris M/2L M/L
In the table, any $ R\leq R_{\hbox{max}}$ suppresses aliasing well.

It is interesting to note that the maximum COLA hop size is double the maximum downsampling factor which avoids aliasing of the main lobe of the window transform in FFT-bin signals $ X_{\tilde m}(\omega_k)$ . Since the COLA constraint is a sufficient condition for perfect reconstruction, this aliasing is quite heavy (see Fig.9.21), yet it is all canceled in the reconstruction. The general theory of aliasing cancellation in perfect reconstruction filter banks will be taken up in Chapter 11.

Figure 9.21: Illustration of main-lobe aliasing intervals.
\includegraphics[width=3in]{eps/WindowAliasingFD}

It is important to realize that aliasing cancellation is disturbed by FBS spectral modifications.10.4For robustness in the presence of spectral modifications, it is advisable to keep $ R\leq R_{\hbox{max}}= M/(2L)$ . For compression, it is common to use $ R = 2 R_{\hbox{max}}= R_{\hbox{\hbox{\sc Cola}}} = M/L$ together with a ``synthesis window'' in a weighted overlap-add (WOLA) scheme (§8.6).

Next Section:
Hop Sizes for WOLA
Previous Section:
Filter Bank Reconstruction