Sines + Noise Modeling

Free Books Spectral Audio Signal Processing

As mentioned in the introduction to this chapter, it takes many sinusoidal components to synthesize noise well (as many as 25 per critical band of hearing under certain conditions [85]). When spectral peaks are that dense, they are no longer perceived individually, and it suffices to match only their statistics to a perceptually equivalent degree.

Sines+Noise (S+N) synthesis [249] generalizes the sinusoidal signal models to include a filtered noise component, as depicted in Fig.10.7. In that figure, white noise is denoted by , and the slowly changing linear filter applied to the noise at time is denoted $h_t(\cdot)$ .

The time-varying spectrum of the signal is said to be made up of a deterministic component (the sinusoids) and a stochastic component (time-varying filtered noise) [246,249]:

$\displaystyle s(t) \eqsp \sum_{i=1}^{N} A_i(t) \cos[ \theta_i(t)] + e(t),$

(11.21)

where and $\theta_i(t)$ are the instantaneous amplitude and phase of the th sinusoidal component, and is the residual, or noise signal, assumed to be well modeled by filtered white noise:

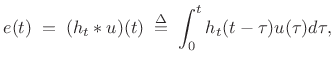$\displaystyle e(t) \eqsp (h_t \ast u)(t) \isdefs \int_0^t h_{t}(t-\tau)u(\tau)d\tau,$

(11.22)

where is the white noise, and $h_t(\tau)$ is the impulse response of a time varying linear filter at time . Specifically, $h_t(\tau)$ is the response at time to an impulse at time $t-\tau$ .

Filtering white-noise to produce a desired timbre is an example of subtractive synthesis [186]. Thus, additive synthesis is nicely supplemented by subtractive synthesis as well.

Sines+Noise Analysis

The original sines+noise analysis method is shown in Fig.10.11 [246,249]. The processing path along the top from left to right measures the amplitude and frequency trajectories from magnitude peaks in the STFT, as in Fig.10.10. The peak amplitude and frequency trajectories are converted back to the time domain by additive-synthesis (an oscillator bank or inverse FFT), and this signal is windowed by the same analysis window and forward-transformed back into the frequency domain. The magnitude-spectrum of this sines-only data is then subtracted from the originally computed magnitude-spectrum containing both peaks and ``noise''. The result of this subtraction is termed the residual signal. The upper spectral envelope of the residual magnitude spectrum is measured using, e.g., linear prediction, cepstral smoothing, as discussed in §10.3 above, or by simply connecting peaks of the residual spectrum with linear segments to form a more traditional (in computer music) piecewise linear spectral envelope.

$\begin{psfrags} % latex2html id marker 27835\psfrag{s}{\Large $x(n)$}\begin{figure}[htbp] \includegraphics[width=\twidth]{eps/smsanal} \caption{Sines+noise analysis diagram (from \cite{SerraT}).} \end{figure} \end{psfrags}$

S+N Synthesis

A sines+noise synthesis diagram is shown in Fig.10.12. The spectral-peak amplitude and frequency trajectories are possibly modified (time-scaling, frequency scaling, virtual formants, etc.) and then rendered into the time domain by additive synthesis. This is termed the deterministic part of the synthesized signal.

The stochastic part is synthesized by applying the residual-spectrum-envelope (a time-varying FIR filter) to white noise, again after possible modifications to the envelope.

To synthesize a frame of filtered white noise, one can simply impart a random phase to the spectral envelope, i.e., multiply it by $\exp[j\phi(\omega_k)]$ , where $\phi(\omega_k)$ is random and uniformly distributed between $-\pi$ and $\pi$ . In the time domain, the synthesized white noise will be approximately Gaussian due to the central limit theorem (§D.9.1). Because the filter (spectral envelope) is changing from frame to frame through time, it is important to use at least 50% overlap and non-rectangular windowing in the time domain. The window can be implemented directly in the frequency domain by convolving its transform with the complex white-noise spectrum (§3.3.5), leaving only overlap-add to be carried out in the time domain. If the window side-lobes can be fully neglected, it suffices to use only main lobe in such a convolution [239].

In Fig.10.12, the deterministic and stochastic components are summed after transforming to the time domain, and this is the typical choice when an explicit oscillator bank is used for the additive synthesis. When the IFFT method is used for sinusoid synthesis [239,94,139], the sum can occur in the frequency domain, so that only one inverse FFT is required.

$\begin{psfrags} % latex2html id marker 27855\psfrag{IFFT} [][c]{{\Large IFFT $\cdot w$}}\begin{figure}[htbp] \includegraphics[width=\twidth]{eps/smssynth} \caption{Sines+noise synthesis diagram (from \cite{SerraT}).} \end{figure} \end{psfrags}$

Sines+Noise Summary

To summarize, sines+noise modeling is carried out by a procedure such as the following:

Compute a sinusoidal model by tracking peaks across STFT frames, producing a set of amplitude envelo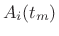pes and frequency envelopes 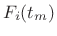, where is the frame number and is the spectral-peak number.
Also record phase 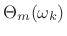$\Theta_m(\omega_k)$ for frames containing a transient.
Subtract modeled peaks from each STFT spectrum to form a residual spectrum.
Fit a smooth spectral envelope $H_m(\omega_k)$ to each residual spectrum.
Convert envelopes to reduced form, e.g., piecewise linear segments with nonuniformly distributed breakpoints (optimized to be maximally sparse without introducing audible distortion).
Resynthesize audio (along with any desired transformations) from the amplitude, frequency, and noise-floor-filter envelopes.
Alter frequency trajectories slightly to hit the desired phase for transient frames (as described below equation Eq. $\,$ (10.19)).

Because the signal model consists entirely of envelopes (neglecting the phase data for transient frames), the signal model is easily time scaled, as discussed further in §10.5 below.

For more information on sines+noise signal modeling, see, e.g., [146,10,223,248,246,149,271,248,271]. A discussion from an historical perspective appears in §G.11.4.

Next Section:
Sines + Noise + Transients Models
Previous Section:
Additive Synthesis Analysis