Additive Synthesis (Early Sinusoidal Modeling)
Additive synthesis is evidently the first technique widely used for
analysis and synthesis of audio in computer music
[232,233,184,186,187].
It was inspired directly by Fourier theory
[264,23,36,150] (which followed Daniel
Bernoulli's insights (§G.1)) which states that any sound
can be expressed mathematically as a sum of sinusoids. The
`term ``additive synthesis'' refers to sound being formed by adding
together many sinusoidal components modulated by relatively
slowly varying amplitude and frequency envelopes:
![$\displaystyle y(t)= \sum\limits_{i=1}^{N} A_i(t)\sin[\theta_i(t)]$](http://www.dsprelated.com/josimages_new/sasp2/img1799.png) |
(11.17) |
where
and all quantities are real. Thus, each sinusoid may have an independently time-varying amplitude and/or phase, in general. The amplitude and frequency envelopes are determined from some kind of short-time Fourier analysis as discussed in Chapters 8 and 9) [62,187,184,186].
An additive-synthesis oscillator-bank is shown in Fig.10.7, as
it is often drawn in computer music [235,234]. Each
sinusoidal oscillator [166]
accepts an amplitude envelope 
(e.g., piecewise linear,
or piecewise exponential) and a frequency envelope 
,
also typically piecewise linear or exponential. Also shown in
Fig.10.7 is a filtered noise input, as used in S+N
modeling (§10.4.3).
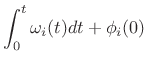
![\begin{psfrags}
% latex2html id marker 27324\psfrag{A1} []{ \Large$ A_1(t)$\ }\psfrag{A2} []{ \Large$ A_2(t)$\ }\psfrag{A3} []{ \Large$ A_3(t)$\ }\psfrag{A4} []{ \Large$ A_4(t)$\ }\psfrag{f1} []{ \Large$ f_1(t)$\ }\psfrag{f2} []{ \Large$ f_2(t)$\ }\psfrag{f3} []{ \Large$ f_3(t)$\ }\psfrag{f4} []{ \Large$ f_4(t)$\ }\psfrag{s} [b]{ {\Huge$\sum$} }\psfrag{noise} [][b]{{\Large$\stackrel{\hbox{[new] noise}}{u(t)}$}}\psfrag{Filter} [][c]{{\Large$\stackrel{\hbox{filter}}{h_t(\tau)}$}}\psfrag{out} []{
{\large$ y(t)= \sum\limits_{i=1}^{4}
A_i(t)\sin\left[\int_0^t\omega_i(t)dt +\phi_i(0)\right]
+ (h_t \ast u)(t) $\ = sine-sum + filtered-noise}}\begin{figure}[htbp]
\includegraphics[width=0.9\twidth]{eps/additive}
\caption{Sinusoidal oscillator bank and filtered
noise for sines+noise spectral modeling synthesis.}
\end{figure}
\end{psfrags}](http://www.dsprelated.com/josimages_new/sasp2/img1810.png)
Next Section:
Additive Synthesis Analysis
Previous Section:
Spectral Envelope Examples
