A Direct Digital Synthesizer with Arbitrary Modulus

Suppose you have a system with a 10 MHz sample clock, and you want to generate a sampled sinewave at any frequency below 5 MHz on 500 kHz spacing; i.e., 0.5, 1.0, 1.5, … MHz.  In other words, f = k*f_s/20, where k is an integer and f_s is sample frequency.  This article shows how to do this using a simple Direct Digital Synthesizer (DDS) with a look-up table that is at most 20 entries long.   We’ll also demonstrate a Quadrature-output DDS.  A note on terminology:  some authors call a DDS a Numerically-Controlled Oscillator (NCO).

Disclaimer:  I have not implemented this DDS in hardware, so there could be problems with the scheme that I have not anticipated.

This article is available in PDF format for easy printing.

Background [1,2]

A continuous-time sinewave with frequency f₀ is given by y = sin(2πf₀t + φ₀).  For a sampled signal, we replace t by nT_s, where n is the sample number and T_s is the sample time.  Letting φ₀ = 0, we have:

y = sin(2πf₀nT_s)

The phase of the signal is:

Φ = 2πf₀nT_s     rad    (mod 2π),

Or

Φ = f₀nT_s    cycles     (mod 1)       (1)

The phase wraps every 2π radians = 1 cycle.  Equation 1 shows that the phase increases (accumulates) by f₀T_s every sample.  So we can calculate the phase using an accumulator with input = f₀T_s, as shown in Figure 1a.  The value of φ has a range of 0 to 1 (cycles).  We generate the sinewave from the phase using a look-up table (LUT).  What we’ve just described is a basic DDS.  Note that another option to generate the sinewave from the phase not discussed here is the CORDiC algorithm [3].

Figure 1b adds quantization in the accumulator register, the phase, and the LUT entries.  The accumulator input has 2^C steps over a range of 0 to 1, giving a frequency step Δf = f_s/2^C, where f_s is the sample frequency.  The resulting output frequencies are f_s/2^C, 2f_s/2^C, 3f_s/2^C …  Given the 2^C steps, we can say the DDS has a modulus of 2^C.  As an example, if C= 24 bits, and f_s= 10 MHz, the frequency step is:

Δf = 10E6/2²⁴ = 0.59605 Hz.

This frequency step is impressively small.  However, if you want to program a frequency that is not on one of the steps, such as f_s/10, there will be a small frequency error of up to Δf/2.

If we were to maintain the 24 bits of phase, the LUT size for this example, taking symmetry of the sine into account, would be ¼*2²⁴ = 2²² = 4,194,304 entries.  To avoid such a large LUT, the phase is normally quantized to P < C bits.  The phase quantization results in so-called phase truncation spurs in the output spectrum.  A typical value of P used in DDS chips is 15 bits, which, taking advantage of the symmetry of the sine, gives LUT size of 2¹³= 8192 entries.

You can see that a standard DDS is not a perfect solution to our problem of generating f₀ = k*f_s/20: it does not produce the exact frequency; it requires a not-so-small LUT; and it has spurs due to truncation of the phase.(Note that there are techniques for reducing phase-truncation spurs [4]).

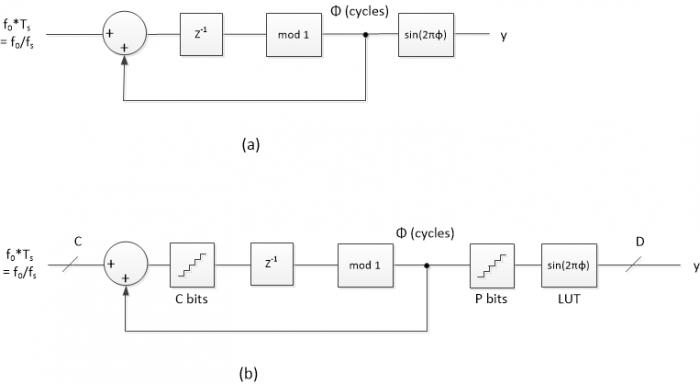
Figure 1.  a)  Implementation of Equation 1.   b)  DDS with quantization.        

DDS with Arbitrary Modulus

A DDS with modulus other than 2^C can address the shortcomings of a conventional DDS for our application.

If we multiply both sides of Equation 1 by an integer L, we get:

LΦ = Lf₀nT_s     (mod L)

This equation can be implemented by modifying the accumulator in Figure 1a as shown in Figure 2.  Here we require m to be an integer between 0 and L-1, so there are L entries in the LUT, where L is not restricted to 2^C.  The input L*f₀/fs is an integer:

L*f₀/fs = k     (2)

or           f₀ = k*fs/L     (3)

Since k is an integer, f₀ has a step size of Δf = fs/L. For a given Δf and fs, we have:

L = fs/Δf     (4)

Letting f_s = 10 MHz and Δf= 0.5 MHz, we get L= 20.  The number of bits required for the accumulator is found by taking log₂(L) and rounding up to the next integer.  For L= 20, we need 5 bits.

As shown in Figure 2, m = Lφ, so the phase is φ = m/L.  Simplistically, the LUT entries are:

u(m) = sin(2πm/L),      m= 0: L-1               (5)

However, for fixed point entries, we need to round the values of u(m) and prevent overflow when m = L/4 and u(L/4) = sin(π/2) = 1.0.  (For example, if the number of bits D= 8, the largest allowable entry is not 1.0 but (2⁷ -1)/2⁷ = 127/128 = 01111111).  We can compute the fixed-point entries as:

u(m) = (1 – ε) * sin(2πm/L),   m= 0: L-1

LUT(m) = round(u(m)*2^D-1)/2^D-1                      (6),

Where D is the number of bits in the 2’s complement LUT entry and ε << 1.  I used ε= 1/2^D-2.  Multiplication by 1 – ε makes the LUT entry for m = L/4 less than 1.0 after rounding. 

For our case, with L= 20, the LUT values are plotted in figure 3.  The LUT contains one cycle of a sinewave evaluated over L samples.  Note that when L is a multiple of 4, it is possible to reduce the LUT size to L/4 entries by taking the symmetry of the sinewave into account.

Figure 2.  DDS with arbitrary modulus

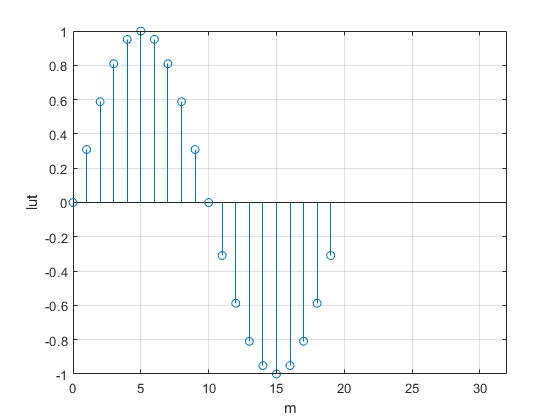
Figure 3.  Sine look-up table for L= 20                 

Let’s look at the behavior of our example DDS, with f_s = 10 Hz and Δf = 0.5 Hz.  The Matlab code is listed in the Appendix.  To start out, let the output frequency f₀= 0.5 Hz.  From equations 2 and 4, k = f₀/Δf, so k= 1.  As shown in Figure 4, m increments through all the integers from 0 to L-1, then repeats.  So the DDS just steps through every entry of the LUT.  Also shown in Figure 4 is the phase φ = m/L cycles, and the sampled sinewave output.

Now, if we let f₀ = 1 Hz, k = 2. Thus m = 0, 2, 4, … and the DDS steps through every 2^nd entry of the LUT, as shown in Figures 5a and 5b.

If we let f₀ = 1. 5 Hz, k= 3.  Thus m= 0, 3, 6, … and the DDS steps through every 3^rd entry of the LUT, as shown in Figures 5c and 5d.  As can be seen in Figure 5c, it takes three cycles for the phase sequence to repeat.

For L= 20, the allowable output frequencies f₀ that are less than f_s/2 are:  0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, and 4.5 Hz, corresponding to k = 1: 9.  For L even, there are L/2 -1 allowable values of f₀.

Since accumulator output m is always an integer, there is no phase truncation error.  The only error in the output y is due to rounding of the LUT entries.  Figure 6 compares spectra for f₀ = 1.5 Hz of a conventional DDS with 15-bits of phase to our DDS with L= 20 (4.3 bits of phase).  Both have 16-bit LUT entries.  The modulus 20 DDS has lower spurious, with the worst spur at about -105 dB with respect to the level at 1.5 Hz.

Finally, note that it is also possible to make a DDS with an arbitrary programmable modulus.The approach involves using two accumulators [5,6].

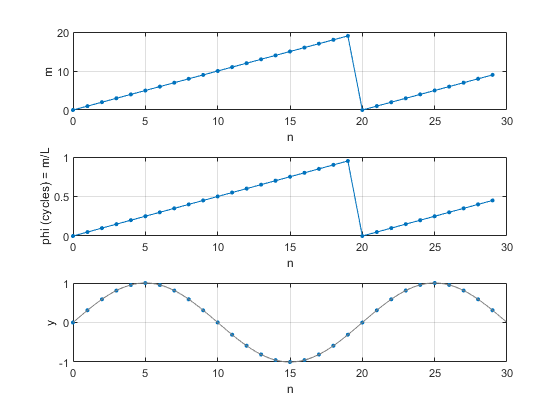
Figure 4.  DDS with L= 20 and f_s = 10 Hz.            

a) Accumulator output m for f₀ = 0.5 Hz.   b) Phase in cycles.   c) LUT output y.

Figure 5.  DDS with L= 20 and f_s = 10 Hz.            

a)  Accumulator output m for f₀ = 1.0 Hz, and

b)  LUT output y                                                   

c)  Accumulator output m for f₀ = 1.5 Hz, and

d)  LUT output y                                                   

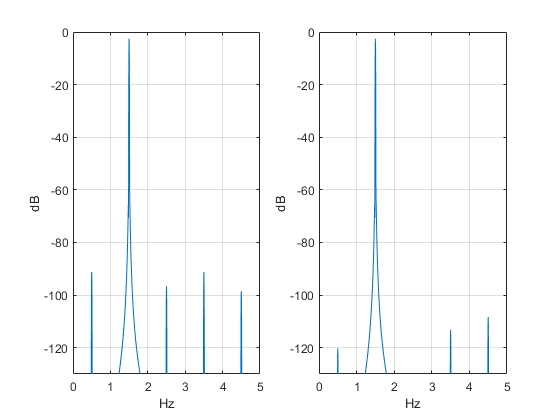
Figure 6. Spectra of conventional DDS and DDS with modulus 20. f₀ = 1.5 Hz and f_s = 10 Hz.

Left:  Conventional DDS with 15 bits of phase and 16-bit LUT entries.

Right:  DDS with L= 20 (4.3 bits of phase) and 16-bit LUT entries.

Quadrature Output DDS

A quadrature output DDS has both cosine and -sine outputs.  The cosine phase leads sine phase by π/2 radians = ¼ cycle.  Given m as the LUT address for a sine, the address for the cosine is:

p = m + L/4   mod(L)

where L is the DDS modulus = LUT length, which must be a multiple of 4.  We can modify the Matlab code in the Appendix to compute both sine and cosine.  Here is the modified for loop:

    sine(1)= 0;
    cosine(1)= 1;
    m= 0;
    for n= 2:N
        r = k + m;
        m= mod(r,L);            % LUT address/ sine
        p= mod(m+ L/4,L);       % LUT address/ cosine
        sine(n)= lut(m+1);      % sine output
        cosine(n)= lut(p+1);    % cosine output
    end

The Quadrature DDS outputs for L= 20, f_s= 10 Hz, and f₀ = 1 Hz are shown in Figure 7.

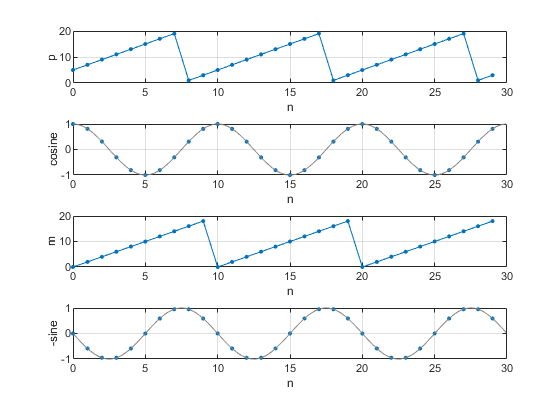
Figure 7.  Quadrature DDS with L= 20, f_s = 10 Hz, and f₀ = 1 Hz.             

           a.  cosine address p.   b) cosine output.   c) sine address m.   d) -sine output.      

Simplest DDS with L= 4

If we let L= 4, there is only one output frequency below f_s/2:

f₀ = k*f_s/L = f_s/4   (k= 1)

The LUT sine values from Equation 5 are:

LUT = [0 sin(π/2) 0 sin(3π/2)]

= [0 1 0 -1]

The cosine values are [1 0 -1 0].

A quadrature L= 4 DDS using cosine and -sine can be used to down-convert a signal centered at f_s/4 to complex baseband [7,8].  Since all LUT values are 0 or +/-1, no multiplier is needed to perform the frequency conversion.

References

1. MT-085, “Fundamentals of Direct Digital Synthesis (DDS)”, Analog Devices, 2009, https://www.analog.com/media/en/training-seminars/tutorials/MT-085.pdf
2. “A Technical Tutorial on Digital Signal Synthesis”, Analog Devices, 1999, https://www.analog.com/media/cn/training-seminars/tutorials/450968421DDS_Tutorial_rev12-2-99.pdf
3. Rice, Michael, Digital Communications, A Discrete-Time Approach, Pearson, 2009, section 9.4.
4. Rice, section 9.2.
5. Gentile, Ken, AN-953, “Direct Digital Synthesis with a Programmable Modulus”, Analog Devices, 2014, https://www.analog.com/media/en/technical-documentation/application-notes/AN-953.pdf
6. Hou, Yuqing, et. al., “An Accurate DDS Method Using Compound Frequency Tuning Word and Its FPGA Implementation”, Electronics, Nov, 2018, https://www.mdpi.com/2079-9292/7/11/330
7. Harris, Fredric J., Multirate Signal Processing, Prentice-Hall PTR, 2004, section 13.2.1.
8. Lyons, Richard G., Understanding Digital Signal Processing, 3^rd Ed., Prentice-Hall, 2011, section 13.1.2.

Neil Robertson      June 3, 2019.  Revised 6/8/19

Appendix    Matlab Code for DDS with Modulus = 20

% dds_mod20.m  5/30/19   Neil Robertson
% DDS with modulus L = 20
% output frequency f0 = k*fs/L
% Plot LUT, phase, and output
fs= 10;                     % Hz sample freq
df= 0.5;                    % Hz desired freq step
L= fs/df                    % length of LUT= modulus of accumulator
if mod(L,1)~=0
    error('fs/fstep must be an integer')
end
% create LUT with one full cycle of sinewave (not using symmetry)
D= 16;                       % bits LUT entries quantization
m= 0:L-1;
phi_lut= m/L;                % cycles phase
epsilon= 1/2^(D-2);
u= (1 - epsilon) *sin(2*pi*phi_lut);
lut= round(u*2^(D-1))/(2^(D-1));      % quantize lut entries
%
% DDS
N= 30;                             % number of output samples
f0= 0.5;                           % Hz output frequency (must be multiple of df)
k= L*f0/fs;                        % integer input to DDS
y(1)= 0;
m= 0;
for n= 2:N
    r = k + m;
    m= mod(r,L);                   % LUT address
    y(n)= lut(m+1);                % output
        phi(n)= m/L;               % cycles phase
end
%
%
% Plotting
%
% plot LUT
stem(0:L-1,lut),grid
axis([0 32 -1 1])
xlabel('m'),ylabel('lut'),figure
%
%plot m and phi
subplot(311),plot(0:N-1,phi*L,'.-','markersize',9),grid
axis([0 N 0 20])
xlabel('n'),ylabel('m')
subplot(312),plot(0:N-1,phi,'.-','markersize',9),grid
axis([0 N 0 1])
xlabel('n'),ylabel('phi (cycles) = m/L')
%
% plot y along with "continuous" sinewave y2 in grey
fs_plot= fs*16;                  % fs of "continuous" sine
Ts= 1/fs_plot;
Len= 16*N;
i= 0:Len-1;
y2= sin(2*pi*f0*i*Ts);           % "continuous" sine
subplot(313),plot(0:N-1,y,'.','markersize',9),grid
hold on
plot(i/16,y2,'color',[.5 .5 .5])
axis([0 N -1 1])
xlabel('n'),ylabel('y')

Sign in