Design study: 1:64 interpolating pulse shaping FIR
This article is the documentation to a code snippet that originated from a discussion on comp.dsp.
The task is to design a root-raised cosine filter with a rolloff of a=0.15 that interpolates to 64x the symbol rate at the input.
The code snippet shows a solution that is relatively straightforward to design and achieves reasonably good efficiency using only FIR filters.
Motivation: “simple solutions?”
The most straightforward approach uses an upsampler (insertion of zero samples) and a long FIR filter. The FIR filter performs a double role for pulse shaping and anti-aliasing.
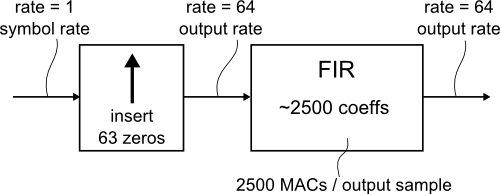
Figure: simple FIR implementation
While unproblematic in Matlab, the solution is not acceptable for any real-life application: 63 out of 64 times, an expensive multiplication is performed with zero, which does not contribute to the output at all. 2500 multiply-and-accumulate (MAC) operations are required for each output sample. That's a lot.
Now the location of zeros in the filter is known at any time. This can be exploited to reorganize the FIR filter into a more efficient polyphase structure:
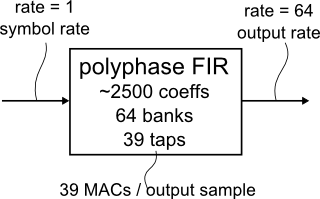
Figure: Polyphase FIR implementation
The computational effort in a polyphase filter reduces to 39 MACs / output sample. The solution is still quite inefficient for a narrow-band signal because the polyphase filter generates every single output sample “from scratch”, based solely on the input data, without utilizing any similarities or common terms between nearby output samples.
Also, the high number of coefficients could be problematic (note that all given coefficient counts could be divided by two in a hardware implementation due to the symmetry of the impulse response)
Proposed filter structure
The implementation from the code snippet takes the following approach:
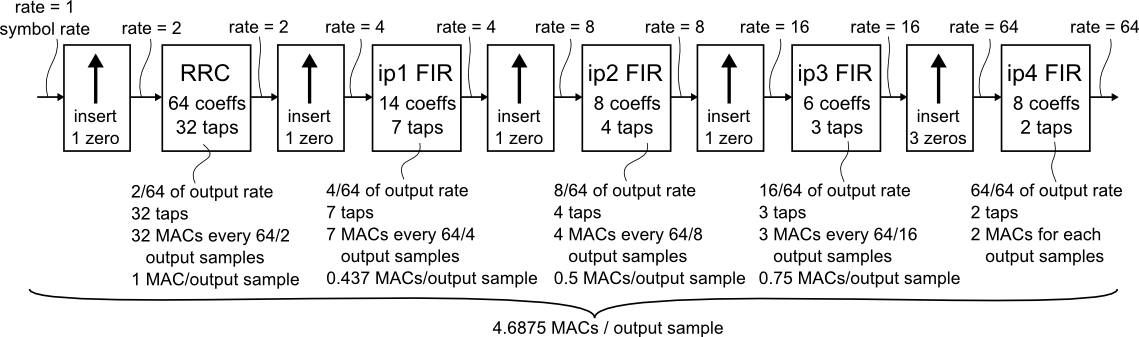
Figure: proposed implementation
It requires only 4.69 MACs/output sample, or 12 % of the polyphase design. The number of coefficients reduces to 102.
The following “features” can be recognized:
-
Pulse shaping filtering and anti-alias filtering for rate conversion are separated.
-
Pulse shaping filtering is performed at the lowest possible integer oversampling factor of two.
-
Each rate conversion stage is designed to suppress aliases only in frequency bands where signal energy is known to be present.
Since the wanted signal and its aliases become relatively narrow-band in later stages, most of the bandwidth turns into “don't-care” regions for filter design, allowing for an efficient implementation.
-
The pulse shaping filter is modified to equalize the non-ideal frequency response of the sample rate conversion stages.
-
All upsamplers (zero insertion) and the following FIR filter are expected to be implemented as polyphase structures.
Further, the “testbench” in eval_RRC_resampler.m shows how to determine the frequency response of a multirate structure and its frequency-dependent in-channel error vector magnitude.
Aliasing
To understand both pulse shape filtering and sample rate conversion, it may be useful to recall that a digital signal represents a sequence of infinitely narrow pulses at the sample locations.
The spectrum contains an infinite number of replicas, or “aliases”, at multiples of the sampling rate:

Figure: A sampled signal. Left: time domain. Right: spectrum
Inserting zeros between existing samples, as done by the upsampler ![]() stages, initially changes nothing:
stages, initially changes nothing:

Figure: Sampled signal after insertion of zero samples (“upsampling”)
While “adding zeros” does not actually alter the signal, the following filter stage gains the ability to change the zero values to non-zero ones:

Figure: upsampled and filtered signal
The following signal illustrates both the spectrum and its periodicity of a narrow-band signal before and after upsampling by a factor of four (insertion of three zero samples per original sample):
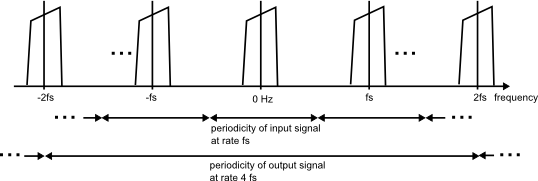
Figure: Periodicity at a signal at different sampling rates
The spectrum remains unchanged, but the following filter stage gains the ability to manipulate aliases independently within the larger bandwidth corresponding to the higher sampling rate (lower arrow).
Design of sample rate conversion stages
The final stage of the design will serve as an example for sample rate conversion. It consists of a 4x upsampler and the “ip4” FIR filter:
The passband is quite narrow in comparison to the output rate of 64. The “ip4” filter is designed for flat gain only within the narrow passband, and stopband attenuation only within the three alias zones. Note that in the drawing, one alias zone appears “split” at both lowest and highest frequencies.
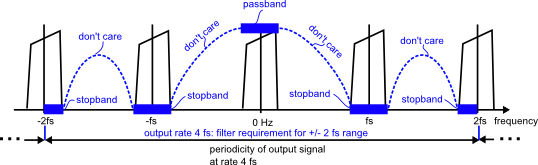
Figure: Filter design specification to selectively suppress narrow-band aliases
Most of the bandwidth is covered by “don't care” regions, where no signal energy is present at the filter input, and the filter response does not matter.
Design of pulse shaping filter
The general idea behind pulse shaping is to take one sample representing a symbol at a time, and generate a narrow-band pulse for transmission. For example, the picture below shows a raised-cosine filter with a=0.5 rolloff.
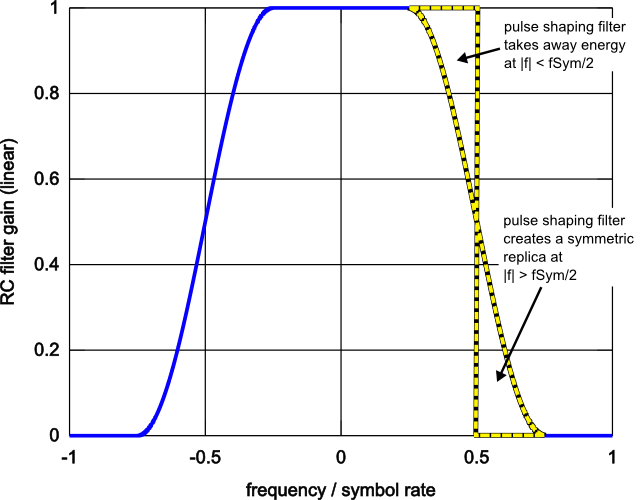
Figure: “textbook” pulse shaping filter frequency response
The filter removes some signal energy within the bandwidth corresponding to the symbol rate (+/- 0.5 in the picture), but allows some excess bandwidth at higher frequencies. If both “corners” are symmetrical, the signal can be sampled without intersymbol interference. Usually, the symmetric response is split between transmitter and receiver ( root-raised cosine filter), and the pulse shaping filter is not exactly symmetrical around the symbol rate.
For an ideal (root)-raised cosine filter, the frequency response is zero for frequencies beyond (1+ a) times the symbol rate.
The signal energy in the “corner” for f > 0.5 originates from the adjacent alias. Thus, the signal in the pulse shaping filter needs to be oversampled to allow independent manipulation of the alias.
The design targets for a pulse shaping filter typically demand a limit on in-band distortion, which is caused by amplitude ripple in a symmetric FIR filter. Further, a spectral emission mask limits unwanted emissions at stopband frequencies. If the signal is intended for wireless transmission and a power amplifier is involved, the pulse shaping filter should be significantly “overdesigned” in the stopband (for example by 10+ dB) to leave more “budget” for distortion products from the power amplifier.
The picture shows the design targets from the RRC_design.m script (download: code snippet) and the resulting frequency response..
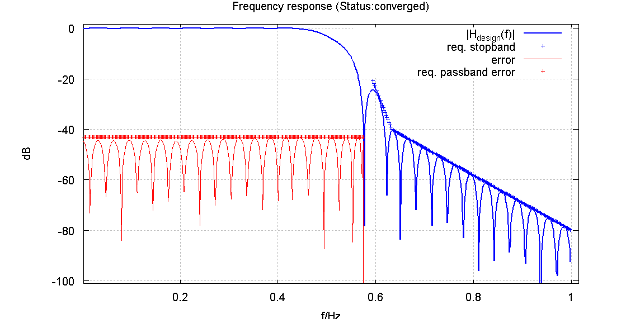
Figure: Design specification of root-raised-cosine pulse shaping filter
Length of impulse responses
The length of a filter's impulse response in seconds is directly related to the transition bandwidth between pass- and stopband, that is, the steepness:
For the pulse shaping filter, the transition bandwidth is quite narrow, about two times 15 % of the sample rate, leading to a relatively long impulse response.
In comparison, the final rate conversion stage is given a transition bandwidth of many times the symbol rate, and its impulse response is accordingly very short.
The following picture shows the individual impulse responses of pulse shaping filter and resampler stages, on a time scale of symbol lengths. The final impulse response (blue) is for the complete design.
It can be clearly seen that the impulse responses of rate conversion stages later in the chain get shorter, as the allowed transition bandwidth gets larger:
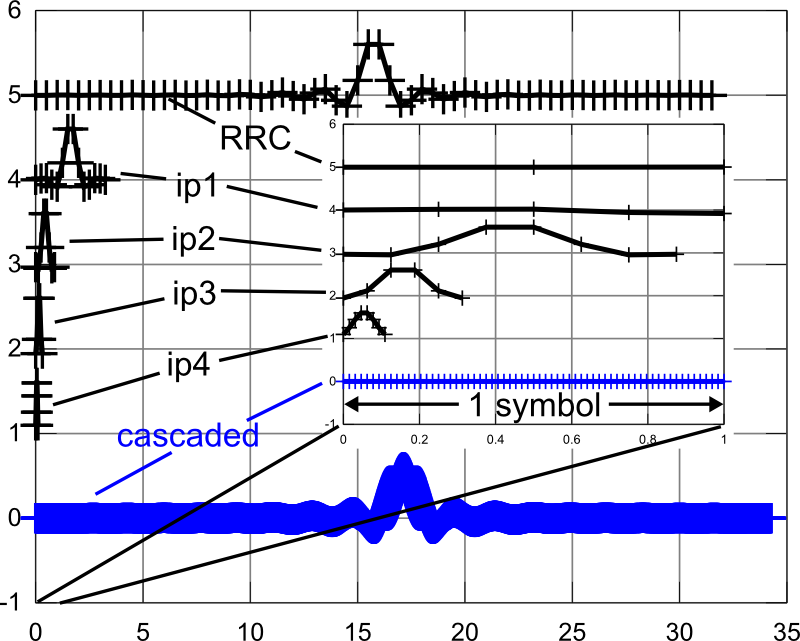
Figure: impulse responses on absolute time axis (in units of symbol durations)
Even though the impulse responses of the final stages are short, they are far from negligible with regard to the computational effort, as they run at a much higher sample rate than the first stages.
As a general rule, it is often a good design strategy is to implement all filtering at the lowest possible rate.
Error simulation
The testbench eval_RRC_resampler.m from the code snippet evaluates the impulse response of the design by performing the upsampling- and filtering operations on a unity pulse test signal. The test signal is longer than the cascaded impulse responses of all stages, thus no truncation error is introduced.
The signal may be considered a regular stream of pulses that repeats after the (arbitrary) length of the test signal). Under that assumption, test signals are cyclic and bandlimited, which allows to represent them exactly via a finite set of Fourier coefficients. Thus, performing a simple FFT will convert freely between time- and frequency domain, without the need for windowing and without introducing error other than numerical inaccuracy.
An ideal root-raised cosine filtered reference signal is acquired by performing RRC-filtering on the test pulse in the frequency domain. Again, under the assumption that the test pulse is one cycle of a periodic sequence, there is no approximation involved: The impulse response has infinite length, but it is allowed to extend into previous and following cycles. It wraps around.
Now with the response of an ideal RRC-filter as reference signal, it is time-aligned with the filter output using the method described here (code here). The difference is considered unwanted signal energy, and can be further divided into in-channel error (distortion to the wanted signal) and aliasing (unwanted emissions at out-of-channel frequencies).
The time alignment minimizes the least-squares difference between the signals. In other words, no other time alignment would result in a a smaller overall error energy.
The spectrum of the in-channel error is plotted. The integrated energy over all frequencies, relative to the wanted signal, gives the error vector magnitude (EVM) in dB. It could be converted to units of percent using EVM_percent = 100*10^(EVM_dB/20).
Design of the first sample rate conversion stage
The pictures show the design specification for the “ip2” sample rate conversion FIR filter, and input/output signals:
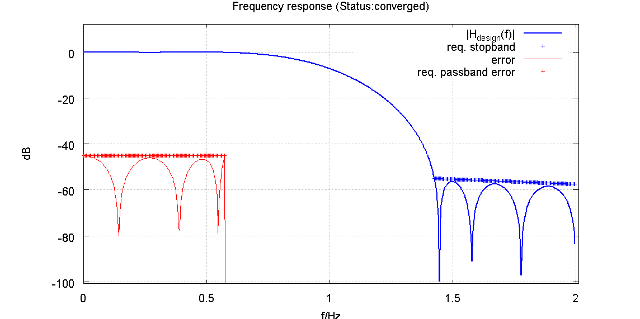
Figure: Design specification for ip1 FIR filter ( run design_ip1.m).
Left +++ line: better than -43 dBc in-channel error at any frequency.
Right +++ line: alias rejection target
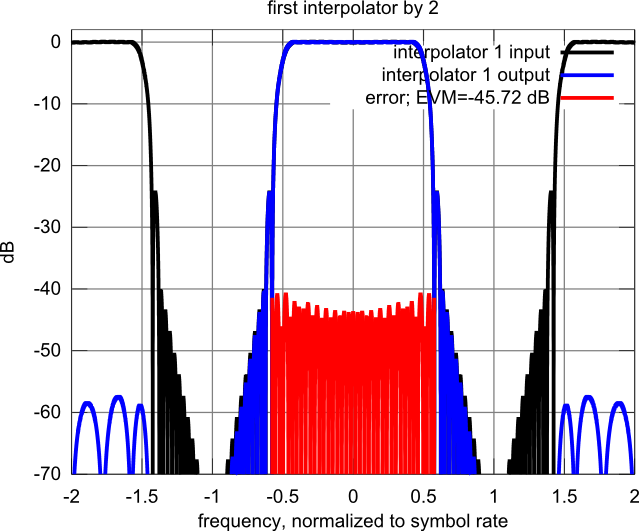
Figure: input signal, output signal and in-channel error signal after the ip1 filter.
Design of the second sample rate conversion stage
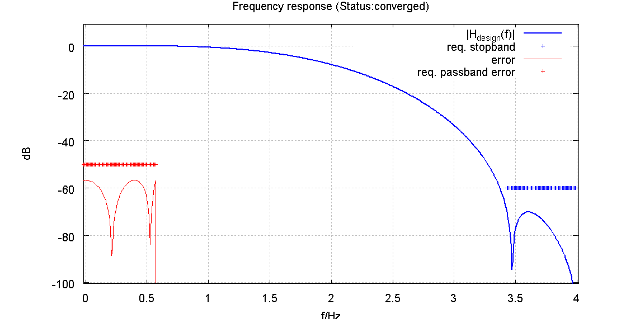
Figure: Design specification of 2 nd interpolator.
Output of “ design_ip2.m”
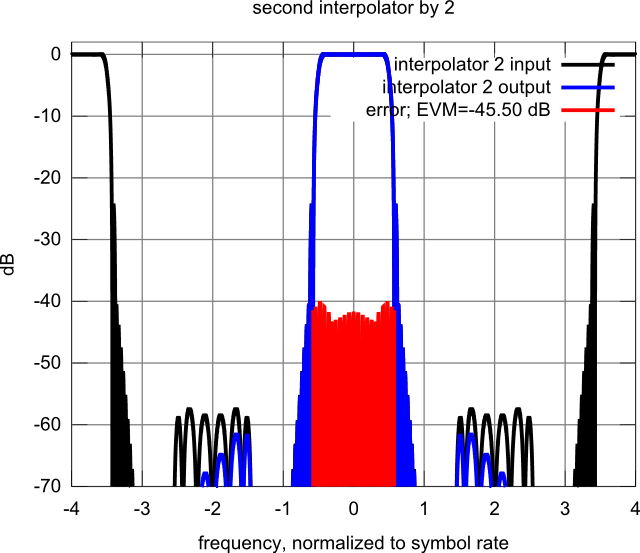
Figure : input signal, output signal and in-channel error signal after the ip2 filter.
Design of the third sample rate conversion stage

Figure: Design specification of third rate conversion stage. Run “ design_ip3.m”
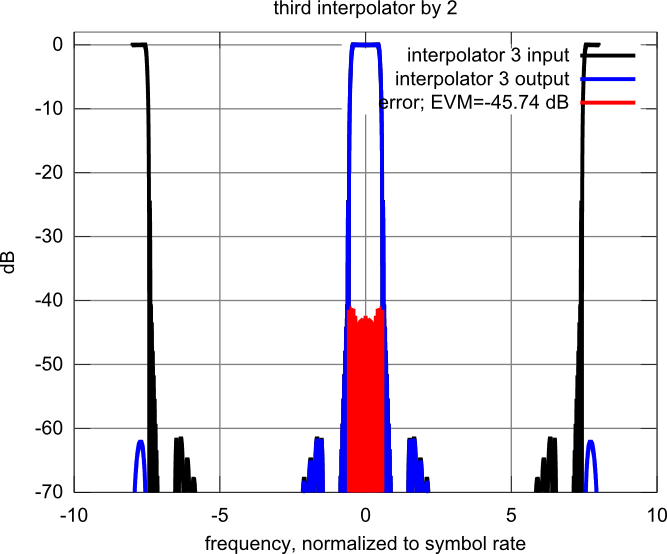
Figure: input signal, output signal and in-channel error signal after the ip3 filter.
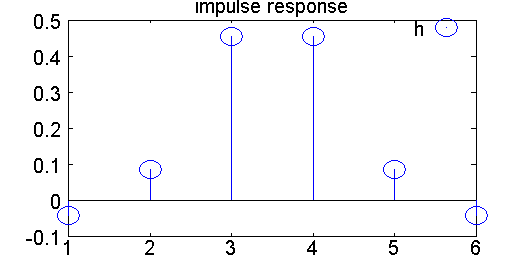
Figure: Impulse response of ip3 filter.
In a polyphase implementation, every second input sample is zero. Three multiplications are required for every output sample.
Design of the fourth sample rate conversion stage
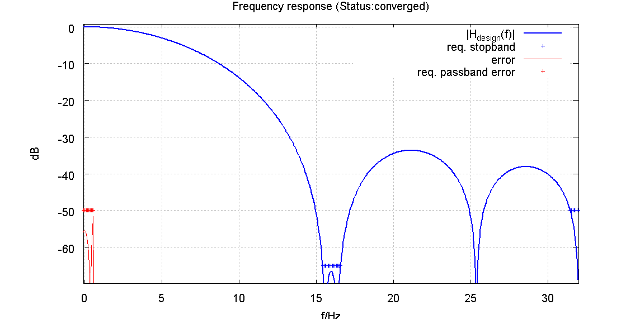
Figure: Design specification of fourth rate conversion stage. Run “ design_ip4.m”
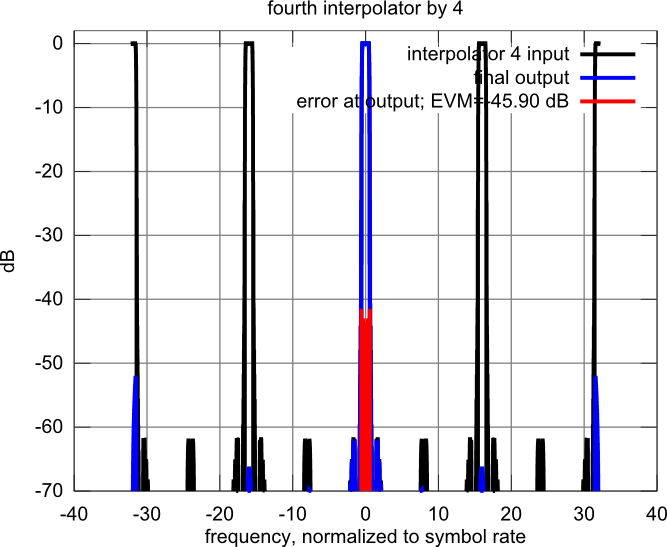
Figure : input signal, output signal and in-channel error signal after the ip3 filter.
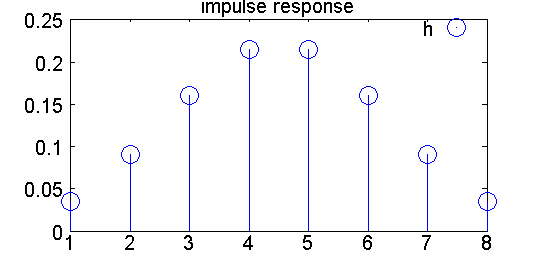
Figure: Impulse response of the final sample rate conversion stage.
Even though the final stage uses only two MAC operations per output sample in a polyphase implementation, it accounts for 42 % of the MAC operations of the whole design. It is a prime candidate for further optimization, for example for replacement with a CIC-type filter.
Equalization
The overall in-channel error is consistent with the design specifications of the individual stages. Nonetheless, at a few frequencies, the errors add up constructively.
The in-band error can be improved by equalizing the frequency response of the sample rate conversion in the pulse shaping filter.
This is implemented in the code snippet as option:
-
Run eval_RRC_resampler with mode="evalIdeal".
The frequency response of the sample rate conversion will be written into interpolatorFrequencyResponse.mat.
-
Run design_RRC_filter with mode=”equalized”. It will design an equalizer with a pre-distorted frequency response into RRC_equalized.dat instead of the conventional RRC.dat file.
-
Re-run eval_RRC_resampler with mode=”evalEqualized” to evaluate the design with the equalized RRC filter.
Use of the equalized pulse shape filter improves the average in-channel error by 1.3 dB and the peak error by more than 3 dB at no additional cost. The downside is that the design process gets more complex.
Lacking accurate requirements, the design has not been optimized extensively for use of equalization. By using equalization more aggressively, it may be feasible to chop away a couple of taps from the rate conversion filters.
The picture below shows the error spectrum at the output of the equalized design:
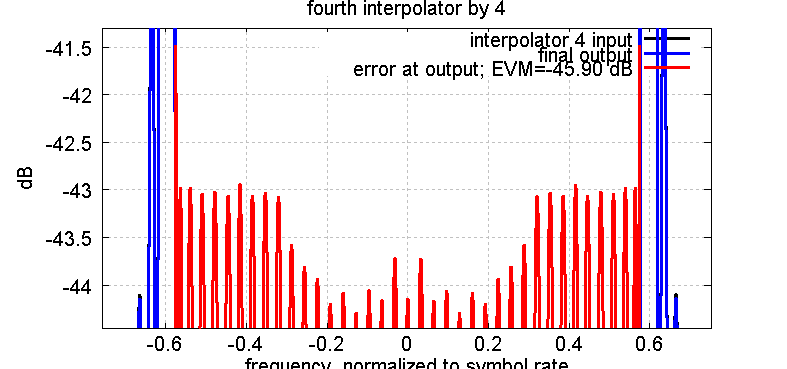
Figure : frequency-dependent in-channel error for the equalized design
The design target for the in-channel error of the equalized RRC filter in design_RRC_filter.m is -43 dB.
Also the simulated peak error at the output of the design from eval_RRC_resampler.m is -43.0 dB. This confirms that the equalized filter works as expected.
Summary
This article describes a design study on a root-raised cosine pulse shape/interpolate-by-64 filter using cascaded FIR stages with the following “features”:
-
Filtering and rate conversion tasks are both specified and implemented separately.
-
All filtering is implemented at the lowest possible rate.
-
The total rate conversion is factored into multiple smaller steps.
-
Lowpass filters suppress only known alias bands.
-
An equalized FIR filter stage is used to reduce distortion on the wanted signal
The design process is somewhat lengthy but in the end quite straightforward, to the point where it could be automated (add a couple of iteration loops to the design scripts to iterate the required number of taps per stage).
At least for the given example, the savings over a plain polyphase implementation are substantial. A further reduction in computational load is possible, if the sample rate conversion is partly replaced with a non-FIR type filter (i.e. CIC).
- Comments
- Write a Comment Select to add a comment





To post reply to a comment, click on the 'reply' button attached to each comment. To post a new comment (not a reply to a comment) check out the 'Write a Comment' tab at the top of the comments.
Please login (on the right) if you already have an account on this platform.
Otherwise, please use this form to register (free) an join one of the largest online community for Electrical/Embedded/DSP/FPGA/ML engineers:


















