Peak to Average Power Ratio and CCDF

• Tutorials

Peak to Average Power Ratio (PAPR) is often used to characterize digitally modulated signals.  One example application is setting the level of the signal in a digital modulator.  Knowing PAPR allows setting the average power to a level that is just low enough to minimize clipping.

However, for a random signal, PAPR is a statistical quantity.  We have to ask, what is the probability of a given peak power?  Then we can decide where to set the average power level such that clipping occurs at an acceptably low rate.

Let Pratio = the ratio of the instantaneous power of a sample to the average power of the signal.  The probability that Pratio exceeds a given value is called the Complementary Cumulative Distribution Function (CCDF).  Given a signal vector x, the CCDF y is computed as follows:

papr = 0:.25:12;         % dB vector of PAPR values
P = x.^2;                % W power of each sample of vector x
Pratio = P/mean(P);      % power/average power
PdB = 10*log10(Pratio);
for i = 1:length(papr)
 y(i) = length(find(PdB >= papr(i)))/N;     % # of samples exceeding papr(i)
end

The figure below shows CCDF for a sine wave and for 100,000 samples of Gaussian noise.  The PAPR of the sine wave is the maximum value vs. the x-axis.  This is of course 20*log10[Vpeak/Vrms] = 20*log10[sqrt(2)] = 3.01 dB.

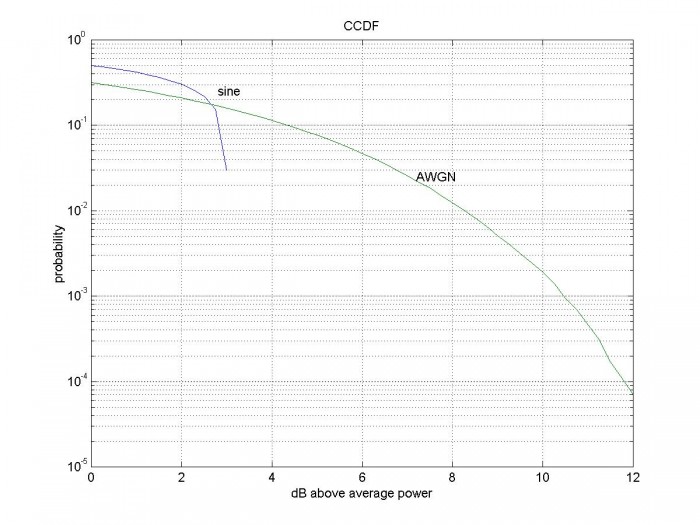
                CCDF of a sine wave and CCDF of AWGN (100,000 samples).

References

“Characterizing Digitally Modulated Signals with CCDF Curves”, Agilent Technologies, 2000.
http://cp.literature.agilent.com/litweb/pdf/5968-6...

%PAPR_demo.m 4/1/16 nr
% PAPR = peak to average power ratio
% Complimentary Cumulative Distribution Function (CCDF) of real signal x.
% x     real signal vector
% papr  vector of papr values
% y     CCDF of x vs. papr
papr = 0:.25:12; % dB vector of PAPR values
% PAPR of sine wave
f = 1; % Hz sine frequency
Ts = 1/1000;                 % s sample time
N= 1000;                     % number of samples
n= 0:N-1;                    % time index
t= n*Ts;                     % s
x = sin(2*pi*f*t);           % signal = one cycle of a sine wave
P = x.^2;                    % W power of each sample of vector x
Pratio = P/mean(P);          % power/average power
PdB = 10*log10(Pratio);
for i = 1:length(papr)
 y(i) = length(find(PdB >= papr(i)))/N;     % # of samples exceeding papr(i)
end
% PAPR of AWGN
randn('state',0);                     % reset random number generator
M = 100000; % number of samples
x_gauss = randn(M,1);                 % signal = AWGN
Pratio = x_gauss.^2;                  % power/average power (average power = 1)
PdB = 10*log10(Pratio);
for i = 1:length(papr)
 y_gauss(i) = length(find(PdB > papr(i)))/M;
end
semilogy(papr,y,papr,y_gauss),grid
xlabel('dB above average power'),ylabel('probability')
title('CCDF'),axis([0 12 1e-5 1])
text(2.8,.25,'sine'),text(7.2,.025,'AWGN')

Sign in