I consider a two-tone input to a nonlinear amplifier.

In a paper I have read (unfortunately I cannot upload the paper), there is a formula mentioned for the calculation of the third order intermodulation distortion of a two-tone input: 

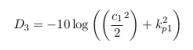
c_1 is the so called amplitude compression and k_p1 is the so called AM-PM conversion factor of the modulation of only one carrier. Here's my question: What does "modulation of only one carrier" mean ? Does it mean, I am changing the frequency of only one carrier and the frequency of the second carrier stays the same? Or does it mean the second carrier is not influenced by any nonlinear distortion?

One would have to read the paper to know what the authors had in mind.  I expect, though, that they meant that they're AM modulating one carrier and seeing how much that AM modulation turns into PM modulation (thus capturing the fact that some nonlinearities affect how quickly an amplifier reacts more than how much it reacts).

Note that the above equation is NOT universal.  It's going to work for amplifiers that tend to distort in ways that the author's amplifiers do.  It may well be good for most class \(\mathrm{AB}_{\mathrm{1}}\) amps, for instance, but not necessarily anything else.  Or it may apply only to bipolar transistors, or only to MOSFETS, or only to good old fashioned toobs.  I'm not enough of an RF guy to know; maybe someone will weigh in.

I do know that I once asked myself "what is the 3rd-order IM behavior of an amplifier that does perfect clipping of the waveform?" -- the answer was "3rd-order IM distortion is a meaningless concept to apply to such amplifiers".

The paper is about TWTAs. And the formula is stated to be valid for a two-tone input. 

Let me see, if I understand your reply correctly: I am given the two-tone input. I am then changing the amplitude of one of the sine-waves, while the amplitude of the other sine-wave stays the same. Now you say, the AM modulation turns into a PM modulation. I don't understand how that is possible, can you explain it? - Maybe for further information: The D3 is the intermodulation distortion, i.e. the power ratio of the signal at the fundamental frequency and the 3rd order intermodulation product.

I suspect that the formula for the AM to PM assumes that you will do that test with just one carrier wave that is amplitude modulated.

Circuits with nonlinear elements in them change their apparent characteristics as the amplitude of the signal through them changes.  I say "apparent characteristics" because the circuit isn't changing -- it's just the best-fit linear model of them changes.  As you drive a larger signal through the amplifier, the amount of lag on that signal changes (it probably gets larger, but you never know).  This, in turn, changes the phase delay.  So, as you amplitude modulate the carrier, the phase shift at the low-amplitude end of things is different from the phase shift at the high-amplitude end of things.

I have absolutely no idea of what nonlinearities exist in a TWT, but if you're having trouble thinking about how any nonlinear system could do this, imagine an otherwise perfect amplifier that has a hard limit on the slope of its output wave.  If you feed it a very small square wave, you'll get a larger, nearly perfect square wave out.  Feed it a large enough square wave, and you'll get a nearly perfect triangle wave out, that's delayed by almost 90 degrees.  A sine wave would have similar effects, although not as pronounced.

Now, take my example amplifier, and run an AM-modulated carrier through it.  The peaks will be delayed from the valleys, so overall the thing will have considerable phase modulation at the output.