Hello,

I had a few questions regarding the inversion properties of convolution and deconvolution in the digital realm (meaning that I'm referring to digital convolution and deconvolution, rather than physical convolution or deconvolution), I was hoping someone could answer.

Question 1: Assuming we start off with the following dry signal:

...is it safe to assume that if we convolve our dry signal with the following IR:

...resulting in the following convolved signal:

...that we would be unable to arrive at our original dry signal via deconvolution (using our same IR), due to the frequency loss that might occur during the convolution of our dry signal and IR?

In other words, if the frequency distribution for our dry signal is:

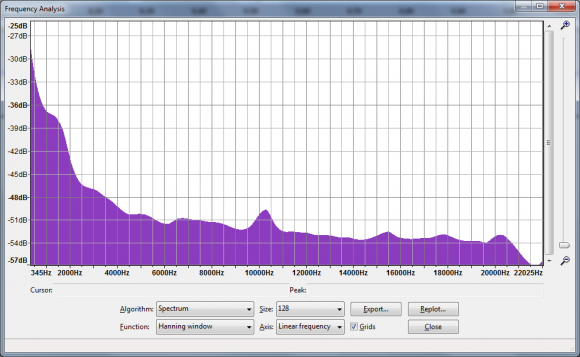
...yet the frequency distribution of our IR is:

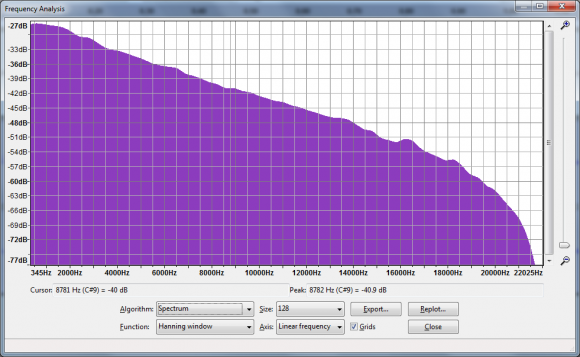
...the lack of frequency data in our IR (see green), but not in our dry signal (see red):

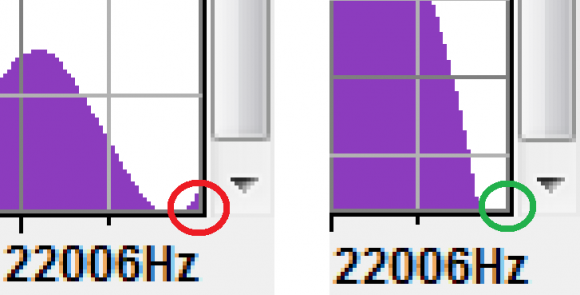
...would result in the loss of that frequency data during convolution?

Question 2: Assuming the answer to question 1 is yes, can I also assume if the frequency distribution for both my dry signal and IR matched, that if I convolved my dry signal with my IR and then deconvolved my convolved signal with the same IR, that I would arrive at the same dry signal?

Question 3: Assuming the answer to question 2 is yes, can I also assume that my frequency distributions really don't have to match exactly?

But rather, what I need to have is just some frequency data in my IR for every place that I have frequency data in my dry signal?

Question 4: Assuming the answer to question 3 is yes, if I simply added the missing frequency data to my IR (via something like an EQ boost).

Would that suffice as a way of adding the missing frequency data to my IR?

Or would I have to use some other method of adding missing frequency data?

If so, what other method would I need to use?

Question 5: Assuming the answers to questions 2 - 4 are no, can I assume that the only way to arrive at our same dry signal, after having been convolved and then deconvolved with the same IR, is to use a chirp signal (please see: https://en.wikipedia.org/wiki/Chirp and http://www.dspguide.com/ch11/6.htm)?

Question 6: If the answer to question 5 is yes, can I assume that there are many chirp signals that one could produce?

In other words, if a chirp signal is just a waveform that increases in frequency by some distribution (ex. linear or exponential) over time:

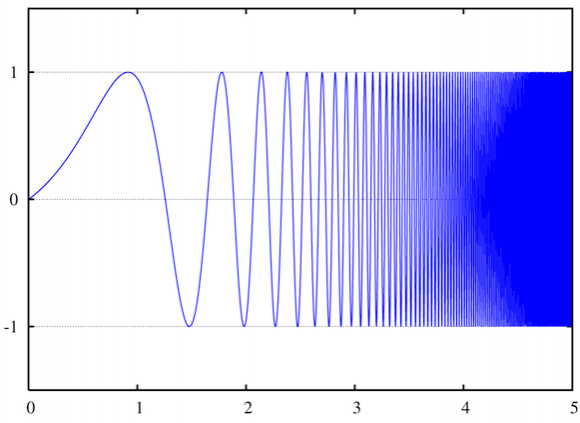
...could we generate a chirp signal using any distribution, or are only certain distributions acceptable?

Question 7: If the answer to question 6 is yes (that we could use any distribution to generate a chirp signal), what distribution would you consider to be the most irregular distribution that one could use to generate a chirp signal?

Question 8: Assuming either the answer to questions 2 - 4 or questions 5 - 6 is yes, what would happen if we performed our convolution and deconvolution in reverse?

What I mean by that is this, if we assume the answers to questions 2 - 4 is yes, then it means that if we had a dry signal:

...and an IR (with either a matching frequency distribution to our dry signal or at the very least, non-zero frequency data for every place we had frequency data in our dry signal):

...and we convolved our dry signal with our IR, resulting in the following convolved signal:

...that if we deconvolved our convolved signal using our same IR, that we'd arrive at the same dry signal:

Note: By "same" dry signal, I mean a sample for sample match of our original dry signal and deconvolved signal.

So my question is this, what would happen if I first deconvolved my dry signal with my IR and then convolved my deconvolved signal with my IR?

Would I arrive at the same dry signal?

In other words, if we likened convolution and deconvolution to something like multiplication and division (i.e. inverse mathematical operations):

If my dry noise signal was the number 6 and my IR was the number 3, and convolving my dry signal by my IR was akin to multiplication, while deconvolution was akin to division, it would mean that:

6 * 3 = 18

If I then deconvolved my convolved signal (ex. 18) by my IR (ex. 3), I'd arrive at:

18 / 3 = 6.

Which would result in my dry signal (i.e. 6).

Conversely, if I deconvolved my dry signal first, I'd arrive at:

6 / 3 = 2

...and then followed that up with convolution, I'd arrive at:

2 * 3 = 6

So the question is, could I arrive at my dry signal using either a frequency matching IR or chirp signal IR, if I deconvolved first and then followed that up with the convolution of my deconvolved signal using the same IR?

Question 9: If the answer to question 8 is no (that either by using a frequency matching IR or chirp signal IR, that I can't arrive at the same dry signal if I deconvolve first and then convolve), is there any way of arriving at my same dry signal using some other non-trivial DSP operation (ex. similar to convolution in complexity)?

Question 10: If the answer to question 9 is yes, what would be the most complex DSP (or even mathematical) operation I could use?

Thank you,
Nelson

Hi nelsona.  I see that your questions were posted two days ago but no one has attempted to reply to you. I think that's because you questions are difficult to understand.  Could you very carefully re-ask your Question# 1 using different words but this time do not sprinkle figures in the middle of the text of your Question# 1?  By the way, what does the word "dry" mean when you write "dry signal"?

Hello Rick,

1. Would you recommend that I break my post into multiple sub-posts (as I'm asking 2 main questions in my main post)?

2. As for the word "dry", it's used to describe an unmolested signal.

For example, in the audio recording / mixing world, a "dry" recording is usually considered to be a recording of a performance without any extra effects.

Whereas a "wet" recording is considered to be a recording that has been affected by one or more effects (ex. compression, limiting, saturation / distortion, delay, reverb, etc).

3. As for my post, it can be summarized into the following two questions.

Question 1: When convolving a dry / unconvolved audio signal, is it safe to assume that if we use an impulse response that is missing frequency data which is found in our dry signal (ex. let's say our dry signal contains frequency data in the 5 Khz - 10 Khz range, but our impulse response does not), that during the convolution phase, frequency data will be lost which cannot be recovered when deconvolving the convolved signal (resulting in a approximate dry / unconvolved audio signal - rather than the exact dry / unconvolved audio signal)?

If that's the case, is it safe to assume if we added the missing frequency data to our impulse response (via an EQ boost for instance), that we would not have lost any frequency data during the convolution phase? Meaning that if we then deconvolved our convolved signal, that'd we'd arrive at the exact same original dry / unconvolved signal (rather than an approximate dry / unconvolved signal - missing some frequency data)?

Question 2: If we start with a dry / unconvolved signal and convolve that signal with an IR, we arrive at a convolved signal. If we then deconvolve that convolved signal, it follows that we should end up with original dry / unconvolved signal (or an estimate of that original dry / unconvolved signal).

What happens if we perform those same operations in reverse?

Will we end up with the same dry / unconvolved signal?

In other words, what happens if we deconvolve a dry / unconvolved signal with an IR, and then convolve the deconvolved signal with the same IR?

Will we end up with the original dry / unconvolved signal?

Example: If we treat convolution as being similar to multiplication (though mathematically it isn't), and deconvolution to be similar to division (though once again, it isn't), if convolution and deconvolution are inversely related, it would follow that whether we used convolution first and then followed that up with deconvolution, that we'd arrive at the same result as if we were to deconvolve first and following that up with convolution.

So hypothetically, if our dry / unconvolved signal is equivalent to the number 3 and our IR is equivalent to the number 6.

Then 3 * 6 = 18 / 6 = 3

...just as:

3 / 6 = 1/2 * 6 = 3

So no matter what order we perform our multiplication (ex. convolution) or division (ex. deconvolution), we arrive at the same final answer.

So the question ultimately is, does this same relation exist for convolution and deconvolution?

Thank you and apologies for the confusion,
Nelson

Hi nelsona.
"Wet" and "dry" huh?  Interesting!  (Sadly, I don't speak the lingo of audio signal processing.) Do you have the word "damp"?  As is in, "That damp signal is not correct!"  (Just jokin'.)

Your Question# 1 is a really interesting question. And I think you've answered that question within the text of your Question# 1.  Here's my thinking:

Let's talk about the notion of you applying some signal sequence, x(n), to an "Effect" (some sort of arithmetic process, such as a filter for example) and that Effect produces a y(n) output signal sequence.  Let's assume the impulse response of your Effect is sequence e(k).  The spectral magnitudes of the Fourier transforms of x(n), e(k), and y(n) are the |X(m)|, |E(m)|, and |Y(m)| curves shown below.

Now if you e-mail the e(k) and y(n) sequences to a friend in California's Folsom State Penitentiary, your friend could try to perform deconvolution (to obtain x(n)) by first computing E(m) and Y(f).  Then he wants to compute the quotient sequence Z(m) = Y(m)/E(m) in the hope of computing the desired x(n) time-domain sequence using:

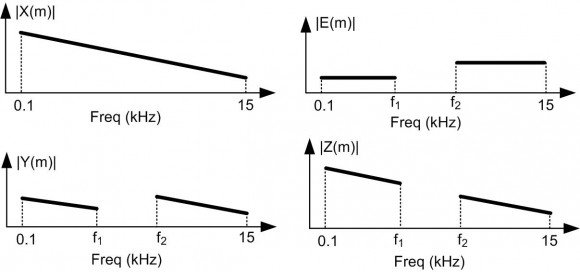
   x(n) = inverse DFT of Z(m) = inverse DFT of Y(m)/E(m).

Not only can your friend not compute the original x(n) sequence, he cannot even compute the Z(m) sequence!  When he tries to compute the Z(m) samples over the freq range of f1 -to- f2 kHz his software will crash because he'll be trying to perform a "divide zero by zero" computation.

 In his prison cell your friend could make his software detect those divide-by-zero operations and set the corresponding  illegal Z(m) quotient samples to zero.  Doing so he'll obtain a Z(m) sequence whose magnitude is shown in my above figure.  That |Z(m)| magnitude plot is somewhat similar to the above |X(m)| plot, but when he computes the inverse DFT of his Z(m) sequence he'll obtain an xo(n) time-domain sequence that is NOT equal to your original x(n). There's no way for your friend to compute the original x(n) sequence.  

For your friend, there's no way for him to "replace" the missing spectral information originally contained within the f1 -to- f2 freq range of X(m) because in your friend's prison cell that missing spectral information (what you call "missing frequency date") does not exist within the Y(m) sequence he received from you!

nelsona, I have to get back to work here.  Let me think more about your Question# 2 and I'll get back to you.  This is an interesting thread, so I hope other guys join in and you do not let it die out too quickly.

Hello Rick,

I can't thank you enough for taking the time to provide me with such a detailed response.

As for question 2, another gentleman answered that question here (https://www.dsprelated.com/thread/5265/what-happen...):

"It seems like you’ve got it right, although your terminology is a bit strange. As you know, if you convolve a signal and then deconvolve it you get the original signal. The reverse is also true, because deconvolution is the same as convolution and the order of operations can be changed without changing the result.

With regards to “what happens”, keep in mind that again, convolution and deconvolution are the same.  For any impulse response, h, there is an impulse response g, such that h convolved with g yields a unit pulse. The caviat being that if h has a zero in its Fourier spectrum, that g may not be realizable."

I had a good idea what the answers to question 1 and 2 were, but I wanted to be 100% certain (as I don't come from the DSP domain - but rather Computer Science).

That being said, any further input would be greatly appreciated.

Thank you and take care,
Nelson