provide an update on this thread:https://www.dsprelated.com/showthread/comp.dsp/236...

But I guess I can't make attachments there.  Probably better anyway since that thread is so old.  Anyway, here are the results from the 11 variants I coded.  Most of these are the resonators published here: http://www.claysturner.com/dsp/ResonatorTable.pdf

output Biquad Goertzel.txt

output Waveguide.txt

output Magic Circle.txt

output Staggered 2.txt

output Coupled.txt

output Reinsch Turner.txt

output Reinsch 0.txt (Staggered)

output Reinsch Pi.txt (Staggered)

output Type A.txt

output Type B.txt

output Type C.txt

output Type C Modified.txt

Another thing these results make me wonder is if there is some disadvantage to the parallel/matrix form.  While they don't seem to have catastophic N^2 error growth, they don't seem to do as well as the staggered forms.  Or maybe it's something about how I coded them?

#Goertzel

instructive and useful. The problem is, it's too difficult to look at a 12 tables of tabular data (with each table containing 76 entries) and make sense out of all that error data. I wonder if it's possible to plot all that error data as curves and present those curves in a way that makes it easy for a reader to visually compare the performance of all those resonators.

Hi Rick.  Thanks for the suggestion.  I have plotted some of these individually (see example below), but I agree that it would be nice to show them in a some comparative form.  Ultimately it would be nice to calculate a big-O error growth for all of these.  That could take a while, because I don't know of any way other than guess and test methods.

Normally the way you'd calculate the error in a linear filter (which is what the Goertzel algorithm is), would be to treat the coefficient quantization as a fixed coefficient error, and treat the data path quantization as noise injected at the points where the quantization happens.

For the coefficients you can just figure out how the frequency and damping ratio deviate from desired.  For the data path quantization you can (hopefully) treat it as white Gaussian noise injected at the points of quantization.

Note that if you're dealing with floating point the quantization gets complicated, because the amplitude grows with growing amplitude in the filter.

Rick,

Here are some error growth numbers comparing the various resonators.  They all seem to fit Err = A*N^x, so I'm publishing the x numbers.  The ones highlighted in green are ones pretty close to O(N).

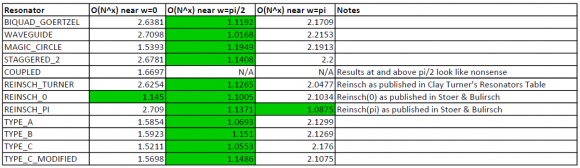
Again, these parallel (non-staggered) update forms seem to be at a disadvantage near 0 and pi.  I could try deriving and implementing a staggered form to see if it makes a difference.

Thanks,

Aaron.