Some time ago, while playing with all kind of approximations of common math functions, I came up to this idea to use a low degree Taylor polynomial for to calculate a1 coefficient for a one pole MZT (Matched Z-transform) based LPF filter:

a1 = −(1.0 + x + 0.5 * x * x)
where
x = 1/(fs*T),
fs = samplerate (Hz),
T = time constant (μs)

so the final filter would be (Octave code):

% --------------------
% OCTAVE PACKAGES 
% --------------------
pkg load signal
% --------------------

clf

fs = 44100;
fc = 10000;
fct= 1/(2 * pi * fc);
fs2= fs/2;
N  = 1;

% ====================
% MZT approximated
% ====================
x = 1.0/(fs*fct); 
MZTa0 = 1.0;
MZTa1 = -(1 + x + 0.5 * x^2); 
MZTb0 = MZTa0 + MZTa1; 
MZTb1 = 0.0; 

MZTa = [MZTa0 MZTa1];
MZTb = [MZTb0 MZTb1];

MZT2=tf(MZTb, MZTa, 1/fs);

% COMPARISONS
% --------------------
% Analog model
% --------------------
w0 = 2*pi*fc;
Analogb = 1;
Analoga = [1 w0];
Analog = tf(Analogb, Analoga);
Analog = Analog/dcgain(Analog);

% --------------------
% MZT
% --------------------
p1 = exp(-1.0/(fs*(1/(2 * pi * fc))))
z1 = 0.0;                            
MZTa0 = 1.0;
MZTa1 = -p1; 
MZTb0 = 1.0-p1;
MZTb1 = -z1; 

MZTa = [MZTa0 MZTa1];
MZTb = [MZTb0 MZTb1];

MZT=tf(MZTb, MZTa, 1/fs);

% --------------------
% IIM
% --------------------
[IIMb,IIMa]=impinvar(Analogb,Analoga,fs); 
IIM=tf(IIMb, IIMa, 1/fs);
IIM=IIM/dcgain(IIM);

% --------------------
% BLT 
% --------------------
w0 = 2*pi*(fc/fs);
%BLTb0 =   sin(w0);
%BLTb1 =   sin(w0);
%BLTa0 =   cos(w0) + sin(w0) + 1.0;
%BLTa1 =   sin(w0) - cos(w0) - 1.0;
%
%BLTa = [BLTa0 BLTa1];
%BLTb = [BLTb0 BLTb1];
%
%BLT=tf(BLTb, BLTa, 1/fs);
%BLT=BLT/dcgain(BLT);

BLT = c2d(Analog, 1/fs, 'prewarp', w0);

% --------------------
% Plot
% --------------------

nf = logspace(0, 5, fs2);

figure(1);
% analog model
[mag, pha] = bode(Analog,2*pi*nf);
semilogx(nf, 20*log10(abs(mag)), 'color', 'g', 'linewidth', 2);
axis([10 fs2 -30 1]);
hold on;
%semilogx(nf, pha, 'color', 'g', 'linewidth', 2, 'linestyle', '--');

% BLT
[mag, pha] = bode(BLT,2*pi*nf);
semilogx(nf, 20*log10(abs(mag)), 'color', 'm', 'linewidth', 1.0, 'linestyle', '-');
%semilogx(nf, pha, 'color', 'm');

% MZT
[mag, pha] = bode(MZT,2*pi*nf);
semilogx(nf, 20*log10(abs(mag)), 'color', 'k', 'linewidth', 1.0, 'linestyle', '-');
%semilogx(nf, pha, 'color', 'k', 'linewidth', 1.0, 'linestyle', '--');

% IIM
[mag, pha] = bode(IIM,2*pi*nf);
semilogx(nf, 20*log10(abs(mag)), 'color', 'c', 'linewidth', 1.0, 'linestyle', '--');
%semilogx(nf, pha, 'color', 'c', 'linewidth', 1.0, 'linestyle', '--');

% MZT approximated
[mag, pha] = bode(MZT2,2*pi*nf);
semilogx(nf, 20*log10(abs(mag)), 'color', 'r', 'linewidth', 2.0, 'linestyle', '--');
%semilogx(nf, -pha, 'color', 'r', 'linewidth', 2.0, 'linestyle', '--');

grid on;

str=num2str(fs);
str2=num2str(fc);
str3=num2str(N);

str = sprintf("LPF (various TF), order:%s, fs=%s, fc=%s, ",str3, str, str2); 
title(str);
legend('Analog', 'BLT', 'MZT', 'IIM', 'MZTapprox', 'location', 'southwest');
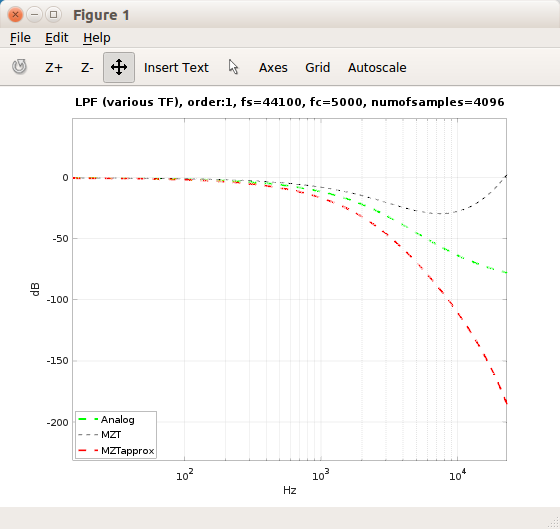
xlabel('Hz');ylabel('dB');

By octave plots

(full sized image), frequency response improves a bit when cut-off frequency is closing fs/2:

and phase response differs a lot from the original MZT phase response:

Idea here is to use approximation error to cancel the error in MZT/IIM (Impulse Invariance Method) methods ... when higher degree polynomial is used the error decreases and the resulting filter closes the original MZT/IIM responses. See the values for s, c and v, v2: https://www.desmos.com/calculator/jvpki1xcvh while changing T parameter.

Someone, with better math skills than what I have, can probably improve this idea by finding better polynomial with suitable error to better cancel the error in MZT/IIM method.

NOTE: There are few well known methods available to improve the MZT/IIM type filters as like these:
    Jackson http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnum...
    Mecklenbräuker http://www.sciencedirect.com/science/article/pii/S...
    Nelatury http://www.sciencedirect.com/science/article/pii/S...
and BLT type filters
    Michael Massberg http://www.aes.org/e-lib/browse.cfm?elib=16077

which all are more complicated and are also more portable methods. My target is speed (realtime use) and improved responses of one pole LPF. I've measured (implementation as c/c++ function) this approximation method about 20 times faster than using std::exp function.

Any thoughts on possible drawbacks in this implementation. Is that phase response a bad thing?

Hi jtp_1960. If you define what your text "MZT/IIM" means, the subscribers here may have some idea what is the topic of your post.

Wiki links added for MZT and IIM.