DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Impulse Response

In the same way that the impulse response of a digital filter is given by the inverse z transform of its transfer function, the impulse response of an analog filter is given by the inverse Laplace transform of its transfer function, viz.,

$\displaystyle h(t) = {\cal L}_t^{-1}\{H(s)\} = \tau e^{-t/\tau} u(t) $

where $ u(t)$ denotes the Heaviside unit step function

$\displaystyle u(t) \isdef \left\{\begin{array}{ll} 1, & t\geq 0 \\ [5pt] 0, & t<0. \\ \end{array}\right. $

This result is most easily checked by taking the Laplace transform of an exponential decay with time-constant $ \tau>0$:

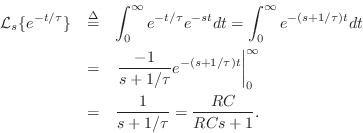
\begin{eqnarray*} {\cal L}_s\{e^{-t/\tau}\} &\isdef & \int_0^{\infty}e^{-t/\tau... ...ght\vert _0^\infty\\ &=& \frac{1}{s+1/\tau} = \frac{RC}{RCs+1}. \end{eqnarray*}

In more complicated situations, any rational $ H(s)$ (ratio of polynomials in $ s$) may be expanded into first-order terms by means of a partial fraction expansion (see §6.8) and each term in the expansion inverted by inspection as above.

Next Section:
The Continuous-Time Impulse
Previous Section:
Transfer Function