DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

RLC Filter Analysis

Referring now to Fig.E.2, let's perform an impedance analysis of that RLC network.

Driving Point Impedance

By inspection, we can write

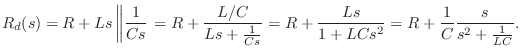
$\displaystyle R_d(s) = R + Ls \left\Vert \frac{1}{Cs}\right. = R +\frac{L/C}{L... ...}{Cs}} = R + \frac{Ls}{1+LCs^2} = R + \frac{1}{C} \frac{s}{s^2+\frac{1}{LC}}. $

where $ \Vert$ denotes ``in parallel with,'' and we used the general formula, memorized by any electrical engineering student,

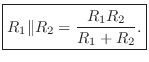
$\displaystyle \zbox {R_1 \Vert R_2 = \frac{R_1 R_2}{R_1 + R_2}.} $

That is, the impedance of the parallel combination of impedances $ R_1$ and $ R_2$ is given by the product divided by the sum of the impedances.

Transfer Function

The transfer function in this example can similarly be found using voltage divider rule:

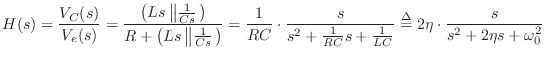
$\displaystyle H(s) = \frac{V_C(s)}{V_e(s)} = \frac{\left(Ls\left\Vert\frac{1}{... ...1}{RC} s + \frac{1}{LC}} \isdef 2\eta\cdot\frac{s}{s^2 + 2\eta s + \omega_0^2} $

Poles and Zeros

From the quadratic formula, the two poles are located at

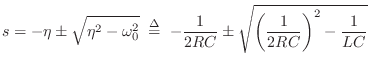
$\displaystyle s = -\eta \pm \sqrt{\eta^2 - \omega_0^2} \;\isdef \; -\frac{1}{2RC} \pm \sqrt{\left(\frac{1}{2RC}\right)^2 - \frac{1}{LC}} $

and there is a zero at $ s=0$ and another at $ s=\infty$. If the damping $ R$ is sufficienly small so that $ \eta^2 < \omega_0^2$, then the poles form a complex-conjugate pair:

$\displaystyle s = -\eta \pm j\sqrt{\omega_0^2 - \eta^2} $

Since $ \eta = 1/(2RC) > 0$, the poles are always in the left-half plane, and hence the analog RLC filter is always stable. When the damping is zero, the poles go to the $ j\omega$ axis:

$\displaystyle s = \pm j\omega_0 $

Impulse Response

The impulse response is again the inverse Laplace transform of the transfer function. Expanding $ H(s)$ into a sum of complex one-pole sections,

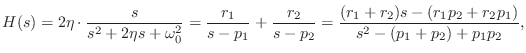
$\displaystyle H(s) = 2\eta\cdot\frac{s}{s^2 + 2\eta s + \omega_0^2} = \frac{r_... ...r_2}{s-p_2} = \frac{(r_1+r_2)s - (r_1p_2 + r_2p_1)}{s^2-(p_1 + p_2) + p_1p_2}, $

where $ p_{1,2}\isdef -\eta \pm \sqrt{\eta^2 - \omega_0^2}$. Equating numerator coefficients gives

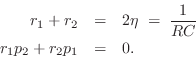
\begin{eqnarray*} r_1+r_2 &=& 2\eta \;\mathrel{=}\; \frac{1}{RC}\\ r_1p_2 + r_2p_1 &=& 0. \end{eqnarray*}

This pair of equations in two unknowns may be solved for $ r_1$ and $ r_2$. The impulse response is then

$\displaystyle h(t) = r_1 e^{p_1 t} u(t) + r_2 e^{p_2 t} u(t). $

Next Section:
Relating Pole Radius to Bandwidth
Previous Section:
RC Filter Analysis