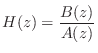Software for Partial Fraction Expansion
Figure 6.3 illustrates the use of residuez (§J.5) for performing a partial fraction expansion on the transfer function
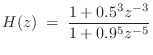
B = [1 0 0 0.125]; A = [1 0 0 0 0 0.9^5]; [r,p,f] = residuez(B,A) % r = % 0.16571 % 0.22774 - 0.02016i % 0.22774 + 0.02016i % 0.18940 + 0.03262i % 0.18940 - 0.03262i % % p = % -0.90000 % -0.27812 - 0.85595i % -0.27812 + 0.85595i % 0.72812 - 0.52901i % 0.72812 + 0.52901i % % f = [](0x0) |
Example 2
For the filter
we obtain the output of residued (§J.6) shown in Fig.6.4. In contrast to residuez, residued delays the IIR part until after the FIR part. In contrast to this result, residuez returns r=[-24;16] and f=[10;2], corresponding to the PFE
| (7.22) |
in which the FIR and IIR parts have overlapping impulse responses.
See Sections J.5 and J.6 starting on page ![]() for
listings of residuez, residued and related
discussion.
for
listings of residuez, residued and related
discussion.
B=[2 6 6 2]; A=[1 -2 1]; [r,p,f,m] = residued(B,A) % r = % 8 % 16 % % p = % 1 % 1 % % f = % 2 10 % % m = % 1 % 2 |
Polynomial Multiplication in Matlab
The matlab function conv (convolution) can be used to perform polynomial multiplication. For example:
B1 = [1 1]; % 1st row of Pascal's triangle B2 = [1 2 1]; % 2nd row of Pascal's triangle B3 = conv(B1,B2) % 3rd row % B3 = 1 3 3 1 B4 = conv(B1,B3) % 4th row % B4 = 1 4 6 4 1 % ...The matlab conv(B1,B2) is identical to filter(B1,1,B2), except that conv returns the complete convolution of its two input vectors, while filter truncates the result to the length of the ``input signal'' B2.7.10 Thus, if B2 is zero-padded with length(B1)-1 zeros, it will return the complete convolution:
B1 = [1 2 3]; B2 = [4 5 6 7]; conv(B1,B2) % ans = 4 13 28 34 32 21 filter(B1,1,B2) % ans = 4 13 28 34 filter(B1,1,[B2,zeros(1,length(B1)-1)]) % ans = 4 13 28 34 32 21
Polynomial Division in Matlab
The matlab function deconv (deconvolution) can be used to perform polynomial long division in order to split an improper transfer function into its FIR and strictly proper parts:
B = [ 2 6 6 2]; % 2*(1+1/z)^3 A = [ 1 -2 1]; % (1-1/z)^2 [firpart,remainder] = deconv(B,A) % firpart = % 2 10 % remainder = % 0 0 24 -8Thus, this example finds that
Bh = remainder + conv(firpart,A) % = 2 6 6 2
The operation deconv(B,A) can be implemented using filter in a manner analogous to the polynomial multiplication case (see §6.8.8 above):
firpart = filter(B,A,[1,zeros(1,length(B)-length(A))]) % = 2 10 remainder = B - conv(firpart,A) % = 0 0 24 -8That this must work can be seen by looking at Eq.
In summary, we may conveniently use convolution and deconvolution to perform polynomial multiplication and division, respectively, such as when converting transfer functions to various alternate forms.
When carrying out a partial fraction expansion on a transfer function having a numerator order which equals or exceeds the denominator order, a necessary preliminary step is to perform long division to obtain an FIR filter in parallel with a strictly proper transfer function. This section describes how an FIR part of any length can be extracted from an IIR filter, and this can be used for PFEs as well as for more advanced applications [].
Separating the Transfer Function Numerator and Denominator
From Eq.![]() (6.5) we have that the transfer function of a
recursive filter is a ratio of polynomials in
(6.5) we have that the transfer function of a
recursive filter is a ratio of polynomials in ![]() :
:
where
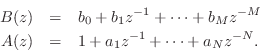
By elementary properties of complex numbers, we have
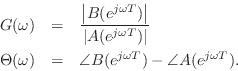
These relations can be used to simplify calculations by hand, allowing the numerator and denominator of the transfer function to be handled separately.
Next Section:
Frequency Response in Matlab
Previous Section:
Summary of the Partial Fraction Expansion








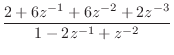
![$\displaystyle (2+10z^{-1}) + z^{-2}\left[\frac{8}{1-z^{-1}} + \frac{16}{(1-z^{-1})^2}\right]
\protect$](http://www.dsprelated.com/josimages_new/filters/img819.png)