Free Books
   Free Books    Introduction to Digital Filters  

Alternative Realizations

For actually implementing the example digital filter, we have only seen the difference equation

$\displaystyle y(n) = x(n) + g_1\, x(n-M_1) - g_2\, y(n-M_2) $

(from Eq.$ \,$(3.1), diagrammed in Fig.3.1). While this structure, formally known as ``direct form I'', happens to be a good choice for digital comb filters, there are many other structures to consider in other situations. For example, it is often desirable, for numerical reasons, to implement low-pass, high-pass, and band-pass filters as series second-order sections. On the other hand, digital filters for simulating the vocal tract (for synthesized voice applications) are typically implemented as parallel second-order sections. (When the order is odd, there is one first-order section as well.) The coefficients of the first- and second-order filter sections may be calculated from the poles and zeros of the filter.

We will now illustrate the computation of a parallel second-order realization of our example filter $ y(n) = x(n) + 0.5^3 x(n-3) - 0.9^5 y(n-5)$. As discussed above in §3.11, this filter has five poles and three zeros. We can use the partial fraction expansion (PFE), described in §6.8, to expand the transfer function into a sum of five first-order terms:

\begin{eqnarray*} H(z) &=& \frac{1 + 0.5^3 z^{-3}}{1 + 0.9^5 z^{-5}} \mathrel{=... ...+} \frac{0.4555 + 0.0922z^{-1}}{1 + 0.5562z^{-1}+ 0.8100z^{-2}}, \end{eqnarray*}

where, in the last step, complex-conjugate one-pole sections are combined into real second-order sections. Also, numerical values are given to four decimal places (so `$ =$' is replaced by `$ \approx$' in the second line). In the following subsections, we will plot the impulse responses and frequency responses of the first- and second-order filter sections above.

First-Order Parallel Sections

Figure 3.13 shows the impulse response of the real one-pole section

$\displaystyle H_1(z) = \frac{0.1657}{1 + 0.9z^{-1}}, $

and Fig.3.14 shows its frequency response, computed using the matlab utility myfreqz listed in §7.5.1. (Both Matlab and Octave have compatible utilities freqz, which serve the same purpose.) Note that the sampling rate is set to 1, and the frequency axis goes from 0 Hz all the way to the sampling rate, which is appropriate for complex filters (as we will soon see). Since real filters have Hermitian frequency responses (i.e., an even amplitude response and odd phase response), they may be plotted from 0 Hz to half the sampling rate without loss of information.

Figure 3.13: Impulse response of section 1 of the example filter.
\includegraphics[width=\twidth]{eps/arir1}

Figure 3.14: Frequency response of section 1 of the example filter.
\includegraphics[width=\twidth]{eps/arfr1}

Figure 3.15 shows the impulse response of the complex one-pole section

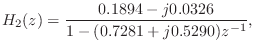
$\displaystyle H_2(z) = \frac{0.1894 - j 0.0326}{1 - (0.7281 + j 0.5290)z^{-1}}, $

and Fig.3.16 shows the corresponding frequency response.

Figure 3.15: Impulse response of complex one-pole section 2 of the full partial-fraction-expansion of the example filter.
\includegraphics[width=\twidth]{eps/arcir2}

Figure 3.16: Frequency response of complex one-pole section 2.
\includegraphics[width=\twidth]{eps/arcfr2}

The complex-conjugate section,

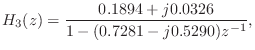
$\displaystyle H_3(z) = \frac{0.1894 + j 0.0326}{1 - (0.7281 - j 0.5290)z^{-1}}, $

is of course quite similar, and is shown in Figures 3.17 and 3.18.

Figure 3.17: Impulse response of complex one-pole section 3 of the full partial-fraction-expansion of the example filter.
\includegraphics[width=\twidth]{eps/arcir3}

Figure 3.18: Frequency response of complex one-pole section 3.
\includegraphics[width=\twidth]{eps/arcfr3}

Figure 3.19 shows the impulse response of the complex one-pole section

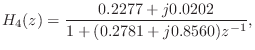
$\displaystyle H_4(z) = \frac{0.2277 + j 0.0202}{1 + (0.2781 + j 0.8560)z^{-1}}, $

and Fig.3.20 shows its frequency response. Its complex-conjugate counterpart, $ H_5(z)$, is not shown since it is analogous to $ H_4(z)$ in relation to $ H_3(z)$.

Figure 3.19: Impulse response of complex one-pole section 4 of the full partial-fraction-expansion of the example filter.
\includegraphics[width=\twidth]{eps/arcir4}

Figure 3.20: Frequency response of complex one-pole section 4.
\includegraphics[width=\twidth]{eps/arcfr4}

Parallel, Real, Second-Order Sections

Figure 3.21 shows the impulse response of the real two-pole section

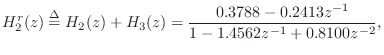
$\displaystyle H^r_2(z) \isdef H_2(z) + H_3(z) = \frac{0.3788 -0.2413z^{-1}}{1 - 1.4562z^{-1}+ 0.8100z^{-2}}, $

and Fig.3.22 shows its frequency response. The frequency axis unnecessarily extends all the way to the sampling rate ($ f_s=1$).

Figure 3.21: Impulse response of real two-pole section $ H^r_2(z)$ of the real partial-fraction-expansion of the example filter.
\includegraphics[width=\twidth]{eps/arir2}

Figure 3.22: Frequency response of real two-pole section $ H^r_2(z)$.
\includegraphics[width=\twidth]{eps/arfr2}

Finally, Fig.3.23 gives the impulse response of the real two-pole section

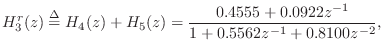
$\displaystyle H^r_3(z) \isdef H_4(z) + H_5(z) = \frac{0.4555 + 0.0922z^{-1}}{1 + 0.5562z^{-1}+ 0.8100z^{-2}}, $

and Fig.3.24 its frequency response.

Figure 3.23: Impulse response of real two-pole section $ H^r_3(z)$ of the real partial-fraction-expansion of the example filter.
\includegraphics[width=\twidth]{eps/arir3}

Figure 3.24: Frequency response of real two-pole section $ H^r_3(z)$.
\includegraphics[width=\twidth]{eps/arfr3}

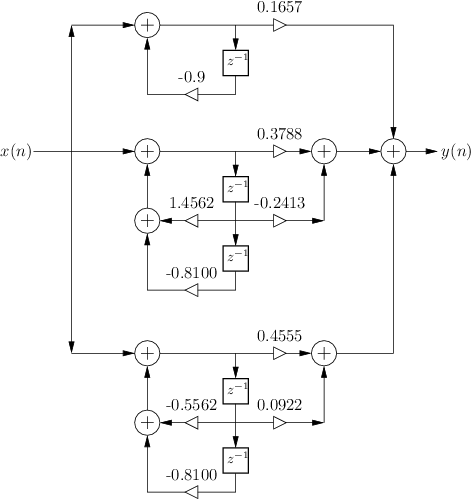
Parallel Second-Order Signal Flow Graph

Figure 3.25 shows the signal flow graph for the implementation of our example filter using parallel second-order sections (with one first-order section since the number of poles is odd). This is the same filter as that shown in Fig.3.1 with $ g_1 = 0.5^3$, $ g_2 = 0.9^5$, $ M_1 = 3$, and $ M_2=5$. The second-order sections are special cases of the ``biquad'' filter section, which is often implemented in software (and chip) libraries. Any digital filter can be implemented as a sum of parallel biquads by finding its transfer function and computing the partial fraction expansion.

Figure 3.25: Signal flow graph for the re-implementation of the example filter $ y(n) = x(n) + 0.5^3 x(n-3) - 0.9^5 y(n-5)$ as a parallel bank of real first- and second-order digital filter sections.
\begin{figure}\input fig/epfe.pstex_t \end{figure}

Figure: Same as Fig.3.25 except using transposed direct-form-II biquad sections in place of direct-form-II biquad sections.
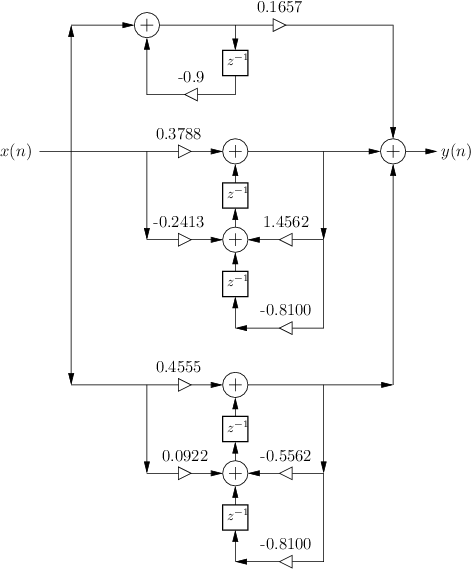\begin{figure}\input fig/epfet.pstex_t \end{figure}

The two second-order biquad sections in Fig.3.25 are in so-called ``Direct-Form II'' (DF-II) form. In Chapter 9, a total of four direct-form filter implementations will be discussed, along with some other commonly used implementation structures. In particular, it is explained there why Transposed Direct-Form II (TDF-II) is usually a better choice of implementation structure for IIR filters when numerical dynamic range is limited (as it is in fixed-point ``DSP chips''). Figure 3.26 shows how our example looks using TDF-II biquads in place of the DF-II biquads of Fig.3.25.

Series, Real, Second-Order Sections

Converting the difference equation $ y(n) = x(n) + 0.5^3 x(n-3) - 0.9^5 y(n-5)$ to a series bank of real first- and second-order sections is comparatively easy. In this case, we do not need a full blown partial fraction expansion. Instead, we need only factor the numerator and denominator of the transfer function into first- and/or second-order terms. Since a second-order section can accommodate up to two poles and two zeros, we must decide how to group pairs of poles with pairs of zeros. Furthermore, since the series sections can be implemented in any order, we must choose the section ordering. Both of these choices are normally driven in practice by numerical considerations. In fixed-point implementations, the poles and zeros are grouped such that dynamic range requirements are minimized. Similarly, the section order is chosen so that the intermediate signals are well scaled. For example, internal overflow is more likely if all of the large-gain sections appear before the low-gain sections. On the other hand, the signal-to-quantization-noise ratio will deteriorate if all of the low-gain sections are placed before the higher-gain sections. For further reading on numerical considerations for digital filter sections, see, e.g., [103].

Next Section:
Summary
Previous Section:
Pole-Zero Analysis