Zero-Phase Filters (Even Impulse Responses)

Free Books Introduction to Digital Filters

Zero-Phase Filters
(Even Impulse Responses)

A zero-phase filter is a special case of a linear-phase filter in which the phase slope is $\alpha=0$ . The real impulse response of a zero-phase filter is even.^11.1 That is, it satisfies

$\displaystyle h(n) = h(-n), \quad n\in{\bf Z}$

Note that every even signal is symmetric, but not every symmetric signal is even. To be even, it must be symmetric about time 0.

A zero-phase filter cannot be causal (except in the trivial case when the filter is a constant scale factor $h(n)=g\delta(n)$ ). However, in many ``off-line'' applications, such as when filtering a sound file on a computer disk, causality is not a requirement, and zero-phase filters are often preferred.

It is a well known Fourier symmetry that real, even signals have real, even Fourier transforms [84]. Therefore,

$\textstyle \parbox{0.8\textwidth}{\emph{a real, even impulse response corresponds to a real, \\ even frequency response.}}$

This follows immediately from writing the DTFT of

in terms of a cosine and sine transform:

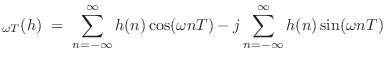
$\displaystyle H(e^{j\omega T}) \eqsp$ DTFT $\displaystyle _{\omega T}(h) \eqsp \sum_{n=-\infty}^\infty h(n) \cos(\omega nT) - j \sum_{n=-\infty}^\infty h(n) \sin(\omega nT)$

Since

is even, cosine is even, and sine is odd; and since even times even is even, and even times odd is odd; and since the sum over an odd function is zero, we have that

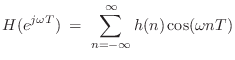
$\displaystyle H(e^{j\omega T}) \eqsp \sum_{n=-\infty}^\infty h(n) \cos(\omega nT)$

for any real, even impulse-response

. Thus, the frequency response $H(e^{j\omega T})$ is a real, even function of $\omega$ .

A real frequency response has phase zero when it is positive, and phase $\pi$ when it is negative. Therefore, we define a zero-phase filter as follows:

$\textstyle \parbox{0.8\textwidth}{A filter is said to be \emph{zero phase} when... ... frequency $\omega$, and when $H(e^{j\omega T})>0$\ in the filter passband(s).}$

Recall from §7.5.2 that a passband is defined as a frequency band that is ``passed'' by the filter, i.e., the filter is not designed to minimize signal amplitude in the band. For example, in a lowpass filter with cut-off frequency $\omega_c$ rad/s, the passband is $\omega\in[-\omega_c,\omega_c]$ .

$\pi$ -Phase Filters

Under our definition, a zero-phase filter always has a real, even impulse response [ ], but not every real, even, impulse response is a zero-phase filter. For example, if is zero phase, then is not; however, we could call a `` $\pi$ -phase filter'' if we like (a zero-phase filter in series with a sign inversion).

Phase $\pi$ in the Stopband

Practical zero-phase filters are zero-phase in their passbands, but may switch between 0 and $\pi$ in their stopbands (as illustrated in the upcoming example of Fig.10.2). Thus, typical zero-phase filters are more precisely described as piecewise constant-phase filters, where the constant phase is 0 in all passbands, and $\pi$ over various intervals within stopbands. Similarly, practical ``linear phase'' filters are typically truly linear phase across their passbands, but typically exhibit discontinuities by $\pi$ radians in their stopband(s). As long as the stopbands are negligible, which is the goal by definition, the $\pi$ -phase regions can be neglected completely.

Example Zero-Phase Filter Design

Figure 10.1 shows the impulse response and frequency response of a length 11 zero-phase FIR lowpass filter designed using the Remez exchange algorithm.^11.2 The matlab code for designing this filter is as follows:

N = 11;                % filter length - must be odd
b = [0 0.1 0.2 0.5]*2; % band edges
M = [1  1   0   0 ];   % desired band values
h = remez(N-1,b,M);    % Remez multiple exchange design

The impulse response h is returned in linear-phase form, so it must be left-shifted

samples to make it zero phase.

**Figure 10.1:** Impulse response and frequency response of a length 11 zero-phase FIR lowpass filter. Note that the frequency response is real because the filter is zero phase. Also plotted (in dashed lines) are the desired passband and stopband gains.
$\includegraphics[width=\twidth ]{eps/remezexa}$

Figure 10.2 shows the amplitude and phase responses of the FIR filter designed by remez. The phase response is zero throughout the passband and transition band. However, each zero-crossing in the stopband results in a phase jump of $\pi$ radians, so that the phase alternates between zero and $\pi$ in the stopband. This is typical of practical zero-phase filters.

**Figure:** Amplitude response and phase response of the length 11 zero-phase FIR lowpass filter in Fig.10.1.
$\includegraphics[width=\twidth ]{eps/remezexb}$

Elementary Zero-Phase Filter Examples

A practical zero-phase filter was illustrated in Figures 10.1 and 10.2. Some simple general cases are as follows:

The trivial (non-)filter 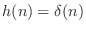$h(n)=\delta(n)$ has frequency response 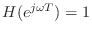$H(e^{j\omega T})=1$ , which is zero phase for all $\omega$ .
Every second-order zero-phase FIR filter has an impulse response of the form

$\displaystyle h(n) \eqsp b_{1}\delta(n+1) + b_0\delta(n) + b_1 \delta(n-1),$
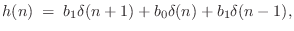
where the coefficients 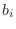are assumed real. The transfer function of the general, second-order, real, zero-phase filter is

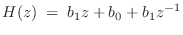$\displaystyle H(z) \eqsp b_{1}z + b_0 + b_1 z^{-1}$
and the frequency response is

$\displaystyle H(e^{j\omega T}) \eqsp b_{1}e^{j\omega T}+ b_0 + b_1 e^{-j\omega T}\eqsp b_0 + 2 b_1 \cos(\omega T)$
which is real for all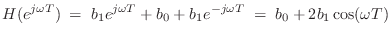 $\omega$ .
Extending the previous example, every order 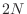zero-phase real FIR filter has an impulse response of the form

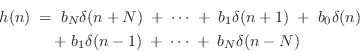
$\begin{eqnarray*} \lefteqn{ h(n) \eqsp b_{N}\delta(n+N) \;+\; \cdots \;+\; b_{... ...ots & & \;+\; b_1 \delta(n-1) \;+\; \cdots \;+\; b_N\delta(n-N) \end{eqnarray*}$

and frequency response

$\displaystyle H(e^{j\omega T}) \eqsp b_0 \;+\; 2 \sum_{k=1}^N b_k \cos(k\omega T)$
which is clearly real whenever the coefficients 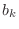are real.
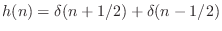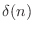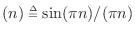There is no first-order (length 2) zero-phase filter, because, to be even, its impulse response would have to be proportional to $h(n)=\delta(n+1/2) + \delta(n-1/2)$ . Since the bandlimited digital impulse signal $\delta (n)$ is ideally interpolated using bandlimited interpolation [91,84], giving samples of sinc $(n)\isdeftext \sin(\pi n)/(\pi n)$ --the unit-amplitude sinc function having zero-crossings on the integers, we see that sampling on the integers yields an IIR filter:

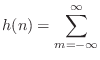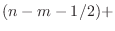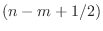
$\displaystyle h(n) = \sum_{m=-\infty}^{\infty}$ sinc $\displaystyle (n-m-1/2) +$ sinc $\displaystyle (n-m+1/2)$
Similarly, there are no odd-order (even-length) zero-phase filters.