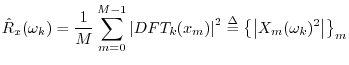Power Spectral Density Estimation
Welch's method [85] (or the periodogram method
[20]) for estimating power spectral densities (PSD) is carried
out by dividing the time signal into successive blocks, and
averaging squared-magnitude DFTs of the signal blocks. Let
![]() ,
,
![]() , denote the
, denote the ![]() th block of the
signal
th block of the
signal
![]() , with
, with ![]() denoting the number of blocks.
Then the Welch PSD estimate is given by
denoting the number of blocks.
Then the Welch PSD estimate is given by
where ``
Recall that
![]() which is
circular (cyclic) autocorrelation. To obtain an acyclic
autocorrelation instead, we may use zero padding in the time
domain, as described in §8.4.2.
That is, we can replace
which is
circular (cyclic) autocorrelation. To obtain an acyclic
autocorrelation instead, we may use zero padding in the time
domain, as described in §8.4.2.
That is, we can replace ![]() above by
above by
![]() .8.12Although this fixes the ``wrap-around problem'', the estimator is
still biased because its expected value is the true
autocorrelation
.8.12Although this fixes the ``wrap-around problem'', the estimator is
still biased because its expected value is the true
autocorrelation ![]() weighted by
weighted by ![]() . This bias is equivalent
to multiplying the correlation in the ``lag domain'' by a
triangular window (also called a ``Bartlett window''). The bias
can be removed by simply dividing it out, as in Eq.
. This bias is equivalent
to multiplying the correlation in the ``lag domain'' by a
triangular window (also called a ``Bartlett window''). The bias
can be removed by simply dividing it out, as in Eq.![]() (8.2), but it is
common to retain the Bartlett weighting since it merely corresponds to
smoothing the power spectrum (or cross-spectrum) with a
sinc
(8.2), but it is
common to retain the Bartlett weighting since it merely corresponds to
smoothing the power spectrum (or cross-spectrum) with a
sinc![]() kernel;8.13it also down-weights the less reliable large-lag
estimates, weighting each lag by the number of lagged products that
were summed.
kernel;8.13it also down-weights the less reliable large-lag
estimates, weighting each lag by the number of lagged products that
were summed.
Since
![]() , and since the DFT
is a linear operator (§7.4.1), averaging
magnitude-squared DFTs
, and since the DFT
is a linear operator (§7.4.1), averaging
magnitude-squared DFTs
![]() is equivalent, in
principle, to estimating block autocorrelations
is equivalent, in
principle, to estimating block autocorrelations
![]() , averaging
them, and taking a DFT of the average. However, this would normally
be slower.
, averaging
them, and taking a DFT of the average. However, this would normally
be slower.
We return to power spectral density estimation in Book IV [70] of the music signal processing series.
Next Section:
Coherence Function
Previous Section:
Correlation Analysis