DSPRelated.com
Free Books
   Free Books    Mathematics of the DFT  

The DFT

This section gives Matlab examples illustrating the computation of two figures in Chapter 6, and the DFT matrix in Matlab.

DFT Sinusoids for 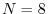$ N=8$

Below is the Matlab for Fig.6.2: 

N=8;
fs=1;

n = [0:N-1]; % row
t = [0:0.01:N]; % interpolated
k=fliplr(n)' - N/2;
fk = k*fs/N;
wk = 2*pi*fk;
clf;
for i=1:N
  subplot(N,2,2*i-1);
  plot(t,cos(wk(i)*t))
  axis([0,8,-1,1]);
  hold on;
  plot(n,cos(wk(i)*n),'*')
  if i==1
    title('Real Part');
  end;
  ylabel(sprintf('k=%d',k(i)));
  if i==N
    xlabel('Time (samples)');
  end;
  subplot(N,2,2*i);
  plot(t,sin(wk(i)*t))
  axis([0,8,-1,1]);
  hold on;
  plot(n,sin(wk(i)*n),'*')
  ylabel(sprintf('k=%d',k(i)));
  if i==1
    title('Imaginary Part');
  end;
  if i==N
    xlabel('Time (samples)');
  end;
end

DFT Bin Response

Below is the Matlab for Fig.6.3: 

% Parameters (sampling rate = 1)
N = 16;               % DFT length
k = N/4;              % bin where DFT filter is centered
wk = 2*pi*k/N;        % normalized radian center-frequency
wStep = 2*pi/N;
w = [0:wStep:2*pi - wStep]; % DFT frequency grid

interp = 10;
N2 = interp*N; % Denser grid showing "arbitrary" frequencies
w2Step = 2*pi/N2;
w2 = [0:w2Step:2*pi - w2Step]; % Extra dense frequency grid
X = (1 - exp(j*(w2-wk)*N)) ./ (1 - exp(j*(w2-wk)));
X(1+k*interp) = N; % Fix divide-by-zero point (overwrite NaN)

% Plot spectral magnitude
clf;
magX = abs(X);
magXd = magX(1:interp:N2); % DFT frequencies only
subplot(2,1,1);
plot(w2,magX,'-'); hold on; grid;
plot(w,magXd,'*');         % Show DFT sample points
title('DFT Amplitude Response at k=N/4');
xlabel('Normalized Radian Frequency (radians per sample)');
ylabel('Magnitude (Linear)');
text(-1,20,'a)');

% Same thing on a dB scale
magXdb = 20*log10(magX);       % Spectral magnitude in dB
% Since the zeros go to minus infinity, clip at -60 dB:
magXdb = max(magXdb,-60*ones(1,N2));
magXddb = magXdb(1:interp:N2); % DFT frequencies only
subplot(2,1,2);
hold off; plot(w2,magXdb,'-'); hold on; plot(w,magXddb,'*');
xlabel('Normalized Radian Frequency (radians per sample)');
ylabel('Magnitude (dB)'); grid;
text(-1,40,'b)');
print -deps '../eps/dftfilter.eps';
hold off;

DFT Matrix

The following example reinforces the discussion of the DFT matrix in §6.12. We can simply create the DFT matrix in matlab by taking the DFT of the identity matrix. Then we show that multiplying by the DFT matrix is equivalent to the calling the fft function in matlab: 

>> eye(4)
ans =
     1     0     0     0
     0     1     0     0
     0     0     1     0
     0     0     0     1

>> S4 = fft(eye(4))
ans =
   1       1          1       1
   1       0 - 1i    -1       0 + 1i
   1      -1          1      -1
   1       0 + 1i    -1       0 - 1i

>> S4' * S4          % Show that S4' = inverse DFT (times N=4)
ans =
    4    0    0    0
    0    4    0    0
    0    0    4    0
    0    0    0    4

>> x = [1; 2; 3; 4]
x =
     1
     2
     3
     4

>> fft(x)
ans =
  10
  -2 + 2i
  -2
  -2 - 2i

>> S4 * x
ans =
  10
  -2 + 2i
  -2
  -2 - 2i

Next Section:
Spectrogram Computation
Previous Section:
Geometric Signal Theory