Free Books Mathematics of the DFT

Derivation of the Discrete Fourier Transform (DFT)

This chapter derives the Discrete Fourier Transform (DFT) as a projection of a length signal onto the set of sampled complex sinusoids generated by the th roots of unity.

Geometric Series

Recall that for any complex number $z_1\in{\bf C}$ , the signal

$\displaystyle x(n)\isdef z_1^n,\quad n=0,1,2,\ldots,$

defines a geometric sequence, i.e., each term is obtained by multiplying the previous term by the (complex) constant

. A geometric series is the sum of a geometric sequence:

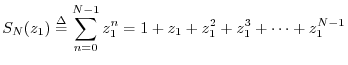
$\displaystyle S_N(z_1) \isdef \sum_{n=0}^{N-1}z_1^n = 1 + z_1 + z_1^2 + z_1^3 + \cdots + z_1^{N-1}$

If $z_1\neq 1$ , the sum can be expressed in closed form:

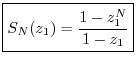
$\displaystyle \zbox {S_N(z_1) = \frac{1-z_1^N}{1-z_1}}$ $\displaystyle \mbox{($z_1\neq 1$)}$

Proof: We have

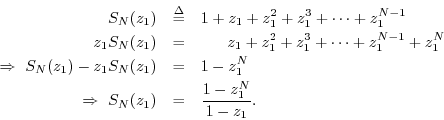
$\begin{eqnarray*} S_N(z_1) &\isdef & 1 + z_1 + z_1^2 + z_1^3 + \cdots + z_1^{N-1... ...z_1^N \\ \,\,\Rightarrow\,\,S_N(z_1) &=& \frac{1-z_1^N}{1-z_1}. \end{eqnarray*}$

When , , by inspection of the definition of .

Orthogonality of Sinusoids

A key property of sinusoids is that they are orthogonal at different frequencies. That is,

$\displaystyle \omega_1 \neq \omega_2 \implies A_1\sin(\omega_1 t + \phi_1) \perp A_2\sin(\omega_2 t + \phi_2).$

This is true whether they are complex or real, and whatever amplitude and phase they may have. All that matters is that the frequencies be different. Note, however, that the durations must be infinity (in general).

For length sampled sinusoidal signal segments, such as used by the DFT, exact orthogonality holds only for the harmonics of the sampling-rate-divided-by-, i.e., only for the frequencies (in Hz)

$\displaystyle f_k = k \frac{f_s}{N}, \quad k=0,1,2,3,\ldots,N-1.$

These are the only frequencies that have a whole number of periods in samples (depicted in Fig.6.2 for

).^6.1

The complex sinusoids corresponding to the frequencies are

$\displaystyle s_k(n) \isdef e^{j\omega_k nT}, \quad \omega_k \isdef k \frac{2\pi}{N}f_s, \quad k = 0,1,2,\ldots,N-1.$

These sinusoids are generated by the

th roots of unity in the complex plane.

Nth Roots of Unity

As introduced in §3.12, the complex numbers

$\displaystyle W_N^k \isdef e^{j\omega_k T} \isdef e^{j k 2\pi (f_s/N) T} = e^{j k 2\pi/N}, \quad k=0,1,2,\ldots,N-1,$

are called the th roots of unity because each of them satisfies

$\displaystyle \left[W_N^k\right]^N = \left[e^{j\omega_k T}\right]^N = \left[e^{j k 2\pi/N}\right]^N = e^{j k 2\pi} = 1.$

In particular,

is called a primitive th root of unity.^6.2

The th roots of unity are plotted in the complex plane in Fig.6.1 for . It is easy to find them graphically by dividing the unit circle into equal parts using points, with one point anchored at , as indicated in Fig.6.1. When is even, there will be a point at (corresponding to a sinusoid with frequency at exactly half the sampling rate), while if is odd, there is no point at .

**Figure 6.1:** The roots of unity for .
$\includegraphics[width=\twidth]{eps/dftfreqs}$

DFT Sinusoids

The sampled sinusoids generated by integer powers of the roots of unity are plotted in Fig.6.2. These are the sampled sinusoids $(W_N^k)^n = e^{j 2 \pi k n / N} = e^{j\omega_k nT}$ used by the DFT. Note that taking successively higher integer powers of the point on the unit circle generates samples of the th DFT sinusoid, giving , $n=0,1,2,\ldots,N-1$ . The th sinusoid generator is in turn the th th root of unity (th power of the primitive th root of unity ).

**Figure 6.2:** Complex sinusoids used by the DFT for .
$\includegraphics[width=\twidth]{eps/dftsines}$

Note that in Fig.6.2 the range of is taken to be instead of . This is the most ``physical'' choice since it corresponds with our notion of ``negative frequencies.'' However, we may add any integer multiple of to without changing the sinusoid indexed by . In other words, $k\pm mN$ refers to the same sinusoid $\exp(j\omega_k nT)$ for all integers .

Orthogonality of the DFT Sinusoids

We now show mathematically that the DFT sinusoids are exactly orthogonal. Let

$\displaystyle s_k(n) \isdef e^{j\omega_k nT} = e^{j2\pi k n /N} = \left[W_N^k\right]^n, \quad n=0,1,2,\ldots,N-1,$

denote the

th DFT complex-sinusoid, for

. Then

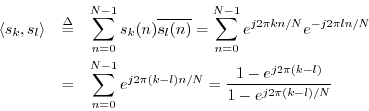
$\begin{eqnarray*} \left<s_k,s_l\right> &\isdef & \sum_{n=0}^{N-1}s_k(n) \overlin... ...i (k-l) n /N} = \frac{1 - e^{j2\pi (k-l)}}{1-e^{j2\pi (k-l)/N}} \end{eqnarray*}$

where the last step made use of the closed-form expression for the sum of a geometric series (§6.1). If $k\neq l$ , the denominator is nonzero while the numerator is zero. This proves

$\displaystyle \zbox {s_k \perp s_l, \quad k \neq l.}$

While we only looked at unit amplitude, zero-phase complex sinusoids, as used by the DFT, it is readily verified that the (nonzero) amplitude and phase have no effect on orthogonality.

Norm of the DFT Sinusoids

For , we follow the previous derivation to the next-to-last step to get

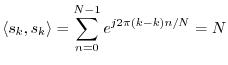
$\displaystyle \left<s_k,s_k\right> = \sum_{n=0}^{N-1}e^{j2\pi (k-k) n /N} = N$

which proves

$\displaystyle \zbox {\left\Vert\,s_k\,\right\Vert = \sqrt{N}.}$

An Orthonormal Sinusoidal Set

We can normalize the DFT sinusoids to obtain an orthonormal set:

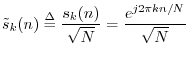
$\displaystyle \tilde{s}_k(n) \isdef \frac{s_k(n)}{\sqrt{N}} = \frac{e^{j2\pi k n /N}}{\sqrt{N}}$

The orthonormal sinusoidal basis signals satisfy

$\displaystyle \left<\tilde{s}_k,\tilde{s}_l\right> = \left\{\begin{array}{ll} 1, & k=l \\ [5pt] 0, & k\neq l. \\ \end{array} \right.$

We call these the normalized DFT sinusoids. In §6.10 below, we will project signals onto them to obtain the normalized DFT (NDFT).

The Discrete Fourier Transform (DFT)

Given a signal $x(\cdot)\in{\bf C}^N$ , its DFT is defined by^6.3

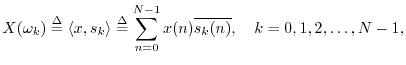
$\displaystyle X(\omega_k) \isdef \left<x,s_k\right> \isdef \sum_{n=0}^{N-1}x(n) \overline{s_k(n)}, \quad k=0,1,2,\ldots,N-1,$

where

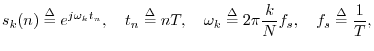
$\displaystyle s_k(n)\isdef e^{j\omega_k t_n}, \quad t_n\isdef nT, \quad \omega_k\isdef 2\pi\frac{k}{N}f_s, \quad f_s\isdef \frac{1}{T},$

or, as it is most often written,

$\displaystyle \zbox {X(\omega_k) \isdef \sum_{n=0}^{N-1}x(n) e^{-j\frac{2\pi k n}{N}}, \quad k=0,1,2,\ldots,N-1.}$

We may also refer to

as the spectrum of

, and $X(\omega_k)$ is the

th sample of the spectrum at frequency $\omega_k$ . Thus, the

th sample $X(\omega_k)$ of the spectrum of

is defined as the inner product of

with the

th DFT sinusoid

. This definition is

times the coefficient of projection of

onto

, i.e.,

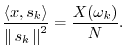
$\displaystyle \frac{\left<x,s_k\right>}{\left\Vert\,s_k\,\right\Vert^2} = \frac{X(\omega_k)}{N}.$

The projection of

onto

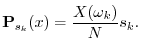
$\displaystyle {\bf P}_{s_k}(x) = \frac{X(\omega_k)}{N} s_k.$

Since the $\{s_k\}$ are orthogonal and span ${\bf C}^N$ , using the main result of the preceding chapter, we have that the inverse DFT is given by the sum of the projections

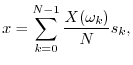
$\displaystyle x = \sum_{k=0}^{N-1}\frac{X(\omega_k)}{N} s_k,$

or, as we normally write,

$\displaystyle \zbox {x(n) = \frac{1}{N} \sum_{k=0}^{N-1}X(\omega_k) e^{j\frac{2\pi k n}{N}}, \quad n=0,1,\ldots,N-1.} \protect$

(6.1)

In summary, the DFT is proportional to the set of coefficients of projection onto the sinusoidal basis set, and the inverse DFT is the reconstruction of the original signal as a superposition of its sinusoidal projections. This basic ``architecture'' extends to all linear orthogonal transforms, including wavelets, Fourier transforms, Fourier series, the discrete-time Fourier transform (DTFT), and certain short-time Fourier transforms (STFT). See Appendix B for some of these.

We have defined the DFT from a geometric signal theory point of view, building on the preceding chapter. See §7.1.1 for notation and terminology associated with the DFT.

Frequencies in the ``Cracks''

The DFT is defined only for frequencies $\omega_k = 2\pi k f_s/N$ . If we are analyzing one or more periods of an exactly periodic signal, where the period is exactly samples (or some integer divisor of ), then these really are the only frequencies present in the signal, and the spectrum is actually zero everywhere but at $\omega=\omega_k$ , $k\in[0,N-1]$ . However, we use the DFT to analyze arbitrary signals from nature. What happens when a frequency $\omega$ is present in a signal that is not one of the DFT-sinusoid frequencies $\omega_k$ ?

To find out, let's project a length segment of a sinusoid at an arbitrary frequency $\omega_x$ onto the th DFT sinusoid:

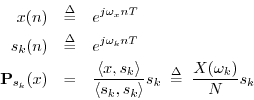
$\begin{eqnarray*} x(n) &\isdef & e^{j\omega_x n T} \\ s_k(n) &\isdef & e^{j\ome... ...}{\left<s_k,s_k\right>}s_k \;\isdef \; \frac{X(\omega_k)}{N}s_k \end{eqnarray*}$

The coefficient of projection is proportional to

$\begin{eqnarray*} X(\omega_k) & \isdef & \left<x,s_k\right> \;\isdef \; \sum_{n=... ...ac{\sin[(\omega_x-\omega_k)NT/2]}{\sin[(\omega_x-\omega_k)T/2]}, \end{eqnarray*}$

using the closed-form expression for a geometric series sum once again. As shown in §6.3-§6.4 above, the sum is if $\omega_k=\omega_x$ and zero at $\omega_l$ , for $l\neq k$ . However, the sum is nonzero at all other frequencies $\omega_x$ .

Since we are only looking at samples, any sinusoidal segment can be projected onto the DFT sinusoids and be reconstructed exactly by a linear combination of them. Another way to say this is that the DFT sinusoids form a basis for ${\bf C}^N$ , so that any length signal whatsoever can be expressed as a linear combination of them. Therefore, when analyzing segments of recorded signals, we must interpret what we see accordingly.

The typical way to think about this in practice is to consider the DFT operation as a digital filter for each , whose input is and whose output is $X(\omega_k)$ at time .^6.4 The frequency response of this filter is what we just computed,^6.5 and its magnitude is

$\displaystyle \left\vert X(\omega_k)\right\vert = \left\vert\frac{\sin[(\omega_x-\omega_k)NT/2]}{\sin[(\omega_x-\omega_k)T/2]}\right\vert$

(shown in Fig.6.3a for

). At all other integer values of

, the frequency response is the same but shifted (circularly) left or right so that the peak is centered on $\omega_k$ . The secondary peaks away from $\omega_k$ are called sidelobes of the DFT response, while the main peak may be called the main lobe of the response. Since we are normally most interested in spectra from an audio perspective, the same plot is repeated using a decibel vertical scale in Fig.6.3b^6.6(clipped at

dB). We see that the sidelobes are really quite high from an audio perspective. Sinusoids with frequencies near $\omega_{k\pm 1.5}$ , for example, are only attenuated approximately

dB in the DFT output $X(\omega_k)$ .

**Figure:** Magnitude frequency response of a particular DFT ``bin'' (where ``bin'' is defined in §6.8). The solid curve shows the relative contribution of arbitrary frequency components to the spectral bin at one-fourth the sampling rate.
$\includegraphics[width=\twidth]{eps/dftfilter}$

We see that $X(\omega_k)$ is sensitive to all frequencies between dc and the sampling rate except the other DFT-sinusoid frequencies $\omega_l$ for $l\neq k$ . This is sometimes called spectral leakage or cross-talk in the spectrum analysis. Again, there is no leakage when the signal being analyzed is truly periodic and we can choose to be exactly a period, or some multiple of a period. Normally, however, this cannot be easily arranged, and spectral leakage can be a problem.

Note that peak spectral leakage is not reduced by increasing .^6.7 It can be thought of as being caused by abruptly truncating a sinusoid at the beginning and/or end of the -sample time window. Only the DFT sinusoids are not cut off at the window boundaries. All other frequencies will suffer some truncation distortion, and the spectral content of the abrupt cut-off or turn-on transient can be viewed as the source of the sidelobes. Remember that, as far as the DFT is concerned, the input signal is the same as its periodic extension (more about this in §7.1.2). If we repeat samples of a sinusoid at frequency $\omega\neq\omega_k$ (for any $k\in{\bf Z}$ ), there will be a ``glitch'' every samples since the signal is not periodic in samples. This glitch can be considered a source of new energy over the entire spectrum. See Fig.8.3 for an example waveform.

To reduce spectral leakage (cross-talk from far-away frequencies), we typically use a window function, such as a ``raised cosine'' window, to taper the data record gracefully to zero at both endpoints of the window. As a result of the smooth tapering, the main lobe widens and the sidelobes decrease in the DFT response. Using no window is better viewed as using a rectangular window of length , unless the signal is exactly periodic in samples. These topics are considered further in Chapter 8.

Spectral Bin Numbers

Since the th spectral sample $X(\omega_k)$ is properly regarded as a measure of spectral amplitude over a range of frequencies, nominally to , this range is sometimes called a frequency bin (as in a ``storage bin'' for spectral energy). The frequency index is called the bin number, and $\left\vert X(\omega_k)\right\vert^2$ can be regarded as the total energy in the th bin (see §7.4.9). Similar remarks apply to samples of any bandlimited function; however, the term ``bin'' is only used in the frequency domain, even though it could be assigned exactly the same meaning mathematically in the time domain.

Fourier Series Special Case

In the very special case of truly periodic signals , for all $t\in(-\infty,\infty)$ , the DFT may be regarded as computing the Fourier series coefficients of from one period of its sampled representation , $n=0,1,\dots,N-1$ . The period of must be exactly seconds for this to work. For the details, see §B.3.

Normalized DFT

A more ``theoretically clean'' DFT is obtained by projecting onto the normalized DFT sinusoids (§6.5)

$\displaystyle \tilde{s}_k(n) \isdef \frac{e^{j2\pi k n/N}}{\sqrt{N}}.$

In this case, the normalized DFT (NDFT) of

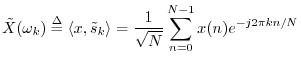
$\displaystyle \tilde{X}(\omega_k) \isdef \left<x,\tilde{s}_k\right> = \frac{1}{\sqrt{N}}\sum_{n=0}^{N-1}x(n) e^{-j2\pi k n/N}$

which is also precisely the coefficient of projection of

onto $\tilde{s}_k$ . The inverse normalized DFT is then more simply

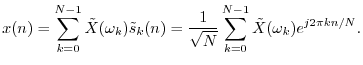
$\displaystyle x(n) = \sum_{k=0}^{N-1}\tilde{X}(\omega_k) \tilde{s}_k(n) = \frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}\tilde{X}(\omega_k)e^{j2\pi k n/N}.$

While this definition is much cleaner from a ``geometric signal theory'' point of view, it is rarely used in practice since it requires slightly more computation than the typical definition. However, note that the only difference between the forward and inverse transforms in this case is the sign of the exponent in the kernel. Advantages of the NDFT over the DFT in fixed-point implementations (Appendix G) are discussed in Appendix A.

It can be said that only the NDFT provides a proper change of coordinates from the time-domain (shifted impulse basis signals) to the frequency-domain (DFT sinusoid basis signals). That is, only the NDFT is a pure rotation in ${\bf C}^N$ , preserving both orthogonality and the unit-norm property of the basis functions. The DFT, in contrast, preserves orthogonality, but the norms of the basis functions grow to $\sqrt{N}$ . Therefore, in the present context, the DFT coefficients can be considered ``denormalized'' frequency-domain coordinates.

The Length 2 DFT

The length DFT is particularly simple, since the basis sinusoids are real:

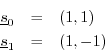
$\begin{eqnarray*} \sv_0 &=& (1,1) \\ \sv_1 &=& (1,-1) \end{eqnarray*}$

The DFT sinusoid $\sv_0$ is a sampled constant signal, while $\sv_1$ is a sampled sinusoid at half the sampling rate.

Figure 6.4 illustrates the graphical relationships for the length DFT of the signal $\underline{x}=[6,2]$ .

**Figure 6.4:** Graphical interpretation of the length 2 DFT.
$\includegraphics[width=\twidth]{eps/dft2}$

Analytically, we compute the DFT to be

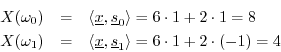
$\begin{eqnarray*} X(\omega_0) &=& \left<\underline{x},\sv_0\right> = 6\cdot 1 + ... ...=& \left<\underline{x},\sv_1\right> = 6\cdot 1 + 2\cdot (-1) = 4 \end{eqnarray*}$

and the corresponding projections onto the DFT sinusoids are

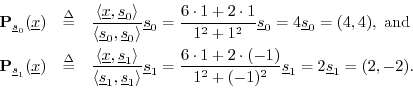
$\begin{eqnarray*} {\bf P}_{\sv_0}(\underline{x}) &\isdef & \frac{\left<\underlin... ...6\cdot 1 + 2 \cdot (-1)}{1^2 + (-1)^2} \sv_1 = 2 \sv_1 = (2,-2). \end{eqnarray*}$

Note the lines of orthogonal projection illustrated in the figure. The ``time domain'' basis consists of the vectors $\{\underline{e}_0,\underline{e}_1\}$ , and the orthogonal projections onto them are simply the coordinate axis projections and . The ``frequency domain'' basis vectors are $\{\sv_0, \sv_1\}$ , and they provide an orthogonal basis set that is rotated degrees relative to the time-domain basis vectors. Projecting orthogonally onto them gives ${\bf P}_{\sv_0}(\underline{x}) = (4,4)$ and ${\bf P}_{\sv_1}(\underline{x}) =(2,-2)$ , respectively. The original signal $\underline{x}$ can be expressed either as the vector sum of its coordinate projections (0,...,x(i),...,0), (a time-domain representation), or as the vector sum of its projections onto the DFT sinusoids (a frequency-domain representation of the time-domain signal $\underline{x}$ ). Computing the coefficients of projection is essentially ``taking the DFT,'' and constructing $\underline{x}$ as the vector sum of its projections onto the DFT sinusoids amounts to ``taking the inverse DFT.''

In summary, the oblique coordinates in Fig.6.4 are interpreted as follows:

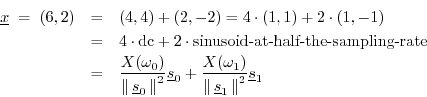
$\begin{eqnarray*} \underline{x}\;=\; (6,2)&=& (4,4)+(2,-2)=4\cdot(1,1)+2\cdot(1,... ..._0 + \frac{X(\omega_1)}{\left\Vert\,\sv_1\,\right\Vert^2}\sv_1 \end{eqnarray*}$

Matrix Formulation of the DFT

The DFT can be formulated as a complex matrix multiply, as we show in this section. (This section can be omitted without affecting what follows.) For basic definitions regarding matrices, see Appendix H.

The DFT consists of inner products of the input signal $\underline{x}$ with sampled complex sinusoidal sections $\sv_k$ :

$\displaystyle X(\omega_k) \isdef \left<\underline{x},\sv_k\right> \isdef \sum_{n=0}^{N-1}\underline{x}(n) e^{-j 2\pi n k/N}, \quad k=0,1,2,\ldots,N-1$

By collecting the DFT output samples into a column vector, we have

$\displaystyle \underbrace{ \left[\begin{array}{c} X(\omega_0) \\ X(\omega_1) ... ... x(2) \\ \vdots \\ x(N-1) \end{array}\right] }_{\displaystyle\underline{x}}$

$\displaystyle \underline{X}= \mathbf{S}^\ast_N \underline{x} = \left[\begin{arr... ...\ [2pt] \vdots \\ [2pt] \left<\underline{x},\sv_{N-1}\right>\end{array}\right]$

where $\mathbf{S}^\ast_N$ denotes the DFT matrix $\mathbf{S}^\ast_N[k,n]\isdef W_N^{-kn} \isdef e^{-j2\pi k n/N}$ , i.e.,

$\begin{eqnarray*} \mathbf{S}^\ast_N &\!\!\isdef \!\!& \left[\begin{array}{cccc}... ...-1)/N} & \cdots & e^{-j 2\pi (N-1)(N-1)/N} \end{array}\!\right]. \end{eqnarray*}$

The notation $A^\ast\isdef \overline{A^{\hbox{\tiny T}}}$ denotes the Hermitian transpose of the complex matrix (transposition and complex conjugation).

Note that the th column of $\mathbf{S}_N$ is the th DFT sinusoid, so that the th row of the DFT matrix $\mathbf{S}^\ast_N$ is the complex-conjugate of the th DFT sinusoid. Therefore, multiplying the DFT matrix times a signal vector $\underline{x}$ produces a column-vector $\underline{X}=\mathbf{S}^\ast_N\underline{x}$ in which the th element $\underline{X}[k]$ is the inner product of the th DFT sinusoid with $\underline{x}$ , or $\underline{X}[k]=\underline{s}^\ast_k\underline{x} = \left<\underline{x},s_k\right>$ , as expected.

Computation of the DFT matrix in Matlab is illustrated in §I.4.3.

The inverse DFT matrix is simply $\mathbf{S}_N/N$ . That is, we can perform the inverse DFT operation as

$\displaystyle \underline{x}= \frac{1}{N} \mathbf{S}_N \underline{X}. \protect$

(6.2)

Since the forward DFT is $\underline{X}=\mathbf{S}^\ast_N\underline{x}$ , substituting $\underline{x}$ from Eq. $\,$ (6.2) into the forward DFT leads quickly to the conclusion that

$\displaystyle \mathbf{S}^\ast_N \mathbf{S}_N = N\cdot \mathbf{I}. \protect$

(6.3)

This equation succinctly states that the columns of $\mathbf{S}_N$ are orthogonal, which, of course, we already knew. I.e., $\left<\sv_k,\sv_n\right>=0$ for $k\ne n$ , and $\left<\sv_k,\sv_k\right>=N$ :

$\begin{eqnarray*} \mathbf{S}^\ast_N \mathbf{S}_N &\!\!=\!\!& \left[\!\begin{arr... ...0 & 0 & 0 & \cdots & N \end{array}\!\right] = N\cdot \mathbf{I}. \end{eqnarray*}$

The normalized DFT matrix is given by

$\displaystyle \tilde{\mathbf{S}}^\ast_{N} \isdef \frac{1}{\sqrt{N}} \mathbf{S}^\ast_{N}$

and the corresponding normalized inverse DFT matrix is simply $\tilde{\mathbf{S}}_N$ , so that Eq. $\,$ (6.3) becomes

$\displaystyle \tilde{\mathbf{S}}^\ast_N \tilde{\mathbf{S}}_N = \mathbf{I}.$

This implies that the columns of $\tilde{\mathbf{S}}_N$ are orthonormal. Such a complex matrix is said to be unitary.

When a real matrix $\mathbf{Q}$ satisfies $\mathbf{Q}^{\!\hbox{\tiny T}}\mathbf{Q}= \mathbf{I}$ , then $\mathbf{Q}$ is said to be orthogonal. ``Unitary'' is the generalization of ``orthogonal'' to complex matrices.