Free Books    Mathematics of the DFT  

Taylor Series Expansions

A Taylor series expansion of a continuous function $ f(x)$ is a polynomial approximation of $ f(x)$. This appendix derives the Taylor series approximation informally, then introduces the remainder term and a formal statement of Taylor's theorem. Finally, a basic result on the completeness of polynomial approximation is stated.

Informal Derivation of Taylor Series

We have a function $ f(x)$ and we want to approximate it using an $ n$th-order polynomial:

$\displaystyle f(x) = f_0 + f_1 x + f_2 x^2 + \cdots + f_n x^n + R_{n+1}(x) $

where $ R_{n+1}(x)$, the approximation error, is called the remainder term. We may assume $ x$ and $ f(x)$ are real, but the following derivation generalizes unchanged to the complex case.

Our problem is to find fixed constants $ \{f_i\}_{i=0}^{n}$ so as to obtain the best approximation possible. Let's proceed optimistically as though the approximation will be perfect, and assume $ R_{n+1}(x)=0$ for all $ x$ ( $ R_{n+1}(x)\equiv0$), given the right values of $ f_i$. Then at $ x=0$ we must have

$\displaystyle f(0) = f_0 $

That's one constant down and $ n-1$ to go! Now let's look at the first derivative of $ f(x)$ with respect to $ x$, again assuming that $ R_{n+1}(x)\equiv0$:

$\displaystyle f^\prime(x) = 0 + f_1 + 2 f_2 x + 3 f_2 x^2 + \cdots + n f_n x^{n-1} $

Evaluating this at $ x=0$ gives

$\displaystyle f^\prime(0) = f_1. $

In the same way, we find

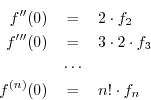
\begin{eqnarray*} f^{\prime\prime}(0) &=& 2 \cdot f_2 \\ f^{\prime\prime\prime}... ...cdot 2 \cdot f_3 \\ & \cdots & \\ f^{(n)}(0) &=& n! \cdot f_n \end{eqnarray*}

where $ f^{(n)}(0)$ denotes the $ n$th derivative of $ f(x)$ with respect to $ x$, evaluated at $ x=0$. Solving the above relations for the desired constants yields

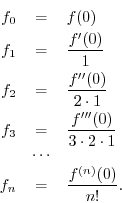
\begin{eqnarray*} f_0 &=& f(0) \\ f_1 &=& \frac{f^{\prime}(0)}{1} \\ f_2 &=& \... ...dot 2\cdot 1} \\ & \cdots & \\ f_n &=& \frac{f^{(n)}(0)}{n!}. \end{eqnarray*}

Thus, defining $ 0!\isdef 1$ (as it always is), we have derived the following polynomial approximation:

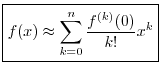
$\displaystyle \zbox {f(x) \approx \sum_{k=0}^n \frac{f^{(k)}(0)}{k!} x^k} $

This is the $ n$th-order Taylor series expansion of $ f(x)$ about the point $ x=0$. Its derivation was quite simple. The hard part is showing that the approximation error (remainder term $ R_{n+1}(x)$) is small over a wide interval of $ x$ values. Another ``math job'' is to determine the conditions under which the approximation error approaches zero for all $ x$ as the order $ n$ goes to infinity. The main point to note here is that the Taylor series itself is simple to derive.

Taylor Series with Remainder

We repeat the derivation of the preceding section, but this time we treat the error term more carefully.

Again we want to approximate $ f(x)$ with an $ n$th-order polynomial:

$\displaystyle f(x) = f_0 + f_1 x + f_2 x^2 + \cdots + f_n x^n + R_{n+1}(x) $

$ R_{n+1}(x)$ is the ``remainder term'' which we will no longer assume is zero.

Our problem is to find $ \{f_i\}_{i=0}^{n}$ so as to minimize $ R_{n+1}(x)$ over some interval $ I$ containing $ x$. There are many ``optimality criteria'' we could choose. The one that falls out naturally here is called Padé approximation. Padé approximation sets the error value and its first $ n$ derivatives to zero at a single chosen point, which we take to be $ x=0$. Since all $ n+1$ ``degrees of freedom'' in the polynomial coefficients $ f_i$ are used to set derivatives to zero at one point, the approximation is termed maximally flat at that point. In other words, as $ x\to0$, the $ n$th order polynomial approximation approaches $ f(x)$ with an error that is proportional to $ \vert x\vert^{n+1}$.

Padé approximation comes up elsewhere in signal processing. For example, it is the sense in which Butterworth filters are optimal [53]. (Their frequency responses are maximally flat in the center of the pass-band.) Also, Lagrange interpolation filters (which are nonrecursive, while Butterworth filters are recursive), can be shown to maximally flat at dc in the frequency domain [82,36].

Setting $ x=0$ in the above polynomial approximation produces

$\displaystyle f(0) = f_0 + R_{n+1}(0) = f_0 $

where we have used the fact that the error is to be exactly zero at $ x=0$ in Padé approximation.

Differentiating the polynomial approximation and setting $ x=0$ gives

$\displaystyle f^\prime(0) = f_1 + R^\prime_{n+1}(0) = f_1 $

where we have used the fact that we also want the slope of the error to be exactly zero at $ x=0$.

In the same way, we find

$\displaystyle f^{(k)}(0) = k! \cdot f_k + R^{(k)}_{n+1}(0) = k! \cdot f_k $

for $ k=2,3,4,\dots,n$, and the first $ n$ derivatives of the remainder term are all zero. Solving these relations for the desired constants yields the $ n$th-order Taylor series expansion of $ f(x)$ about the point $ x=0$

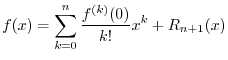
$\displaystyle f(x) = \sum_{k=0}^n \frac{f^{(k)}(0)}{k!} x^k + R_{n+1}(x) $

as before, but now we better understand the remainder term.

From this derivation, it is clear that the approximation error (remainder term) is smallest in the vicinity of $ x=0$. All degrees of freedom in the polynomial coefficients were devoted to minimizing the approximation error and its derivatives at $ x=0$. As you might expect, the approximation error generally worsens as $ x$ gets farther away from 0.

To obtain a more uniform approximation over some interval $ I$ in $ x$, other kinds of error criteria may be employed. Classically, this topic has been called ``economization of series,'' or simply polynomial approximation under different error criteria. In Matlab or Octave, the function polyfit(x,y,n) will find the coefficients of a polynomial $ p(x)$ of degree n that fits the data y over the points x in a least-squares sense. That is, it minimizes

$\displaystyle \left\Vert\,R_{n+1}\,\right\Vert^2 \isdef \sum_{i=1}^{n_x} \left\vert y(i) - p(x(i))\right\vert^2 $

where $ n_x \isdef {\tt length(x)}$.

Formal Statement of Taylor's Theorem

Let $ f(x)$ be continuous on a real interval $ I$ containing $ x_0$ (and $ x$), and let $ f^{(n)}(x)$ exist at $ x$ and $ f^{(n+1)}(\xi)$ be continuous for all $ \xi\in I$. Then we have the following Taylor series expansion:

\begin{eqnarray*} f(x) = f(x_0) &+& \frac{1}{1}f^\prime(x_0)(x-x_0) \\ [10pt] &... ...&+& \frac{1}{n!}f^{(n+1)}(x_0)(x-x_0)^n\\ [10pt] &+& R_{n+1}(x) \end{eqnarray*}

where $ R_{n+1}(x)$ is called the remainder term. Then Taylor's theorem [63, pp. 95-96] provides that there exists some $ \xi$ between $ x$ and $ x_0$ such that

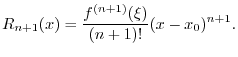
$\displaystyle R_{n+1}(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}. $

In particular, if $ \vert f^{(n+1)}\vert\leq M$ in $ I$, then

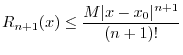
$\displaystyle R_{n+1}(x) \leq \frac{M \vert x-x_0\vert^{n+1}}{(n+1)!} $

which is normally small when $ x$ is close to $ x_0$.

When $ x_0=0$, the Taylor series reduces to what is called a Maclaurin series [56, p. 96].

Weierstrass Approximation Theorem

The Weierstrass approximation theorem assures us that polynomial approximation can get arbitrarily close to any continuous function as the polynomial order is increased.

Let $ f(x)$ be continuous on a real interval $ I$. Then for any $ \epsilon>0$, there exists an $ n$th-order polynomial $ P_n(f,x)$, where $ n$ depends on $ \epsilon$, such that

$\displaystyle \left\vert P_n(f,x) - f(x)\right\vert < \epsilon $

for all $ x\in I$.

For a proof, see, e.g., [63, pp. 146-148].

Thus, any continuous function can be approximated arbitrarily well by means of a polynomial. This does not necessarily mean that a Taylor series expansion can be used to find such a polynomial since, in particular, the function must be differentiable of all orders throughout $ I$. Furthermore, there can be points, even in infinitely differentiable functions, about which a Taylor expansion will not yield a good approximation, as illustrated in the next section. The main point here is that, thanks to the Weierstrass approximation theorem, we know that good polynomial approximations exist for any continuous function.

Points of Infinite Flatness

Consider the inverted Gaussian pulse,E.1

$\displaystyle f(x) \isdef e^{-1/x^2}, % \frac{1}{x^2}}, $

i.e., $ f(1/x)$ is the well known Gaussian ``bell curve'' $ e^{-x^2}$. Clearly, derivatives of all orders exist for all $ x$. However, it is readily verified that all derivatives at $ x=0$ are zero. (It is easier to verify that all derivatives of the bell curve are zero at $ x=\infty$.) Therefore, every finite-order Maclaurin series expansion of $ f(x)$ is the zero function, and the Weierstrass approximation theorem cannot be fulfilled by this series.

As mentioned in §E.2, a measure of ``flatness'' is the number of leading zero terms in a function's Taylor expansion (not counting the first (constant) term). Thus, by this measure, the bell curve is ``infinitely flat'' at infinity, or, equivalently, $ f(x)$ is infinitely flat at $ x=0$.

Another property of $ f(x) \isdef e^{-\frac{1}{x^2}}$ is that it has an infinite number of ``zeros'' at $ x=0$. The fact that a function $ g(x)$ has an infinite number of zeros at $ x=x_0$ can be verified by showing

$\displaystyle \lim_{x\to x_0} \frac{1}{(x-x_0)^k} g(x) = 0 $

for all $ k=1,2,\dots\,$. For $ f(x)$, the existence of an infinite number of zeros at $ x=0$ is easily shown by looking at the zeros of $ f(1/x)$ at $ x=\infty$, i.e.,

$\displaystyle \lim_{x\to\infty} x^k f(1/x) = \lim_{x\to\infty} x^k e^{-x^2} = 0 $

for any integer $ k$. Thus, the faster-than-exponential decay of a Gaussian bell curve cannot be outpaced by the factor $ x^k$, for any finite $ k$. In other words, exponential growth or decay is faster than polynomial growth or decay. (As mentioned in §3.10, the Taylor series expansion of the exponential function $ e^x$ is $ 1 + x + x^2/2 + x^3/3! + \dots$--an ``infinite-order'' polynomial.)

The reciprocal of a function containing an infinite-order zero at $ x=x_0$ has what is called an essential singularity at $ x=x_0$ [15, p. 157], also called a non-removable singularity. Thus, $ 1/f(x) = e^{\frac{1}{x^2}}$ has an essential singularity at $ x=0$, and $ e^{x^2}$ has one at $ x=\infty$.

An amazing result from the theory of complex variables [15, p. 270] is that near an essential singular point $ z_0\in{\bf C}$ (i.e., $ z_0$ may be a complex number), the inequality

$\displaystyle \left\vert f(z)-c\right\vert<\epsilon $

is satisfied at some point $ z\neq z_0$ in every neighborhood of $ z_0$, however small! In other words, the function comes arbitrarily close to every possible value in any neighborhood about an essential singular point. This result, too, is due to Weierstrass [15].

In summary, a Taylor series expansion about the point $ x=x_0$ will always yield a constant approximation when the function being approximated is infinitely flat at $ x_0$. For this reason, polynomial approximations are often applied over a restricted range of $ x$, with constraints added to provide transitions from one interval to the next. This leads to the general subject of splines [81]. In particular, cubic spline approximations are composed of successive segments which are each third-order polynomials. In each segment, four degrees of freedom are available (the four polynomial coefficients). Two of these are usually devoted to matching the amplitude and slope of the polynomial to one side, while the other two are used to maximize some measure of fit across the segment. The points at which adjacent polynomial segments connect are called ``knots'', and finding optimal knot locations is usually a relatively expensive, iterative computation.

Differentiability of Audio Signals

As mentioned in §3.6, every audio signal can be regarded as infinitely differentiable due to the finite bandwidth of human hearing. That is, given any audio signal $ x(t)$, its Fourier transform is given by

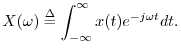
$\displaystyle X(\omega)\isdef \int_{-\infty}^\infty x(t) e^{-j\omega t} dt . $

For the Fourier transform to exist, it is sufficient that $ x(t)$ be absolutely integrable, i.e., $ \int_{-\infty}^\infty\left\vert x(t)\right\vert dt<\infty$. Clearly, all audio signals in practice are absolutely integrable. The inverse Fourier transform is then given by

$\displaystyle x(t) = \frac{1}{2\pi}\int_{-\infty}^\infty X(\omega) e^{j\omega t} d\omega. \protect$

Because hearing is bandlimited to, say, $ 20$ kHz, $ x(t)$ sounds identical to the bandlimited signal

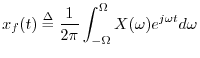
$\displaystyle x_f(t) \isdef \frac{1}{2\pi} \int_{-\Omega}^\Omega X(\omega) e^{j\omega t} d\omega $

where $ \Omega\isdef 2\pi\cdot 20,000$. Now, taking time derivatives is simple (see also §C.1):

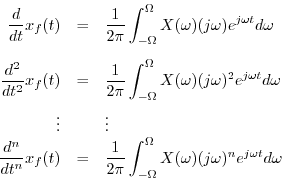
\begin{eqnarray*} \frac{d}{dt} x_f(t) &=& \frac{1}{2\pi} \int_{-\Omega}^\Omega X... ...int_{-\Omega}^\Omega X(\omega) (j\omega)^n e^{j\omega t} d\omega \end{eqnarray*}

Since the length of the integral is finite, there is no possibility that it can ``blow up'' due to the weighting by $ \omega^n$ in the frequency domain introduced by differentiation in the time domain.

A basic Fourier property of signals and their spectra is that a signal cannot be both time limited and frequency limited. Therefore, by conceptually ``lowpass filtering'' every audio signal to reject all frequencies above $ 20$ kHz, we implicitly make every audio signal last forever! Another way of saying this is that the ``ideal lowpass filter `rings' forever''. Such fine points do not concern us in practice, but they are important for fully understanding the underlying theory. Since, in reality, signals can be said to have a true beginning and end, we must admit that all signals we really work with in practice have infinite-bandwidth. That is, when a signal is turned on or off, there is a spectral event extending all the way to infinite frequency (while ``rolling off'' with frequency and having a finite total energy).E.2

In summary, audio signals are perceptually equivalent to bandlimited signals, and bandlimited signals are infinitely smooth in the sense that derivatives of all orders exist at all points time $ t\in(-\infty,\infty)$.

Next Section:
Logarithms and Decibels
Previous Section:
Sampling Theory