Free Books    Mathematics of the DFT  

Logarithms and Decibels

This appendix provides an introduction to logarithms (real and complex) and decibels, a quantitative measure of sound intensity. Several specific dB scales are defined, and dynamic range considerations in audio are considered.

Logarithms

A logarithm $ y=\log_b(x)$ is fundamentally an exponent $ y$ applied to a specific base $ b$ to yield the argument $ x$. That is, $ x = b^y$. The term ``logarithm'' can be abbreviated as ``log''. The base $ b$ is chosen to be a positive real number, and we normally only take logs of positive real numbers $ x>0$ (although it is ok to say that the log of 0 is $ -\infty$). The inverse of a logarithm is called an antilogarithm or antilog; thus, $ x$ is the antilog of $ y$ in the base $ b$.

For any positive number $ x$, we have

$\displaystyle x = b^{\log_b(x)} $

for any valid base $ b>0$. This is just an identity arising from the definition of the logarithm, but it is sometimes useful in manipulating formulas.

When the base is not specified, it is normally assumed to be $ 10$, i.e., $ \log(x) \isdef \log_{10}(x)$. This is the common logarithm.

Base 2 and base $ e$ logarithms have their own special notation:

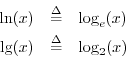
\begin{eqnarray*} \ln(x) &\isdef & \log_e(x) \\ \lg(x) &\isdef & \log_2(x) \end{eqnarray*}

(The use of $ \lg()$ for base $ 2$ logarithms is common in computer science. In mathematics, it may denote a base $ 10$ logarithm.) By far the most common bases are $ 10$, $ e$, and $ 2$. Logs base $ e$ are called natural logarithms. They are ``natural'' in the sense that

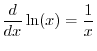
$\displaystyle \frac{d}{dx}\ln(x) = \frac{1}{x} $

while the derivatives of logarithms to other bases are not quite so simple:

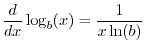
$\displaystyle \frac{d}{dx}\log_b(x) = \frac{1}{x\ln(b)} $

The inverse of the natural logarithm $ y=\ln(x)$ is of course the exponential function $ x=e^y$, and $ e^y$ is its own derivative.

In general, a logarithm $ y$ has an integer part and a fractional part. The integer part is called the characteristic of the logarithm, and the fractional part is called the mantissa. These terms were suggested by Henry Briggs in 1624. ``Mantissa'' is a Latin word meaning ``addition'' or ``make weight''--something added to make up the weight [28].

The following Matlab code illustrates splitting a natural logarithm into its characteristic and mantissa: 

>> x = log(3)
   x = 1.0986
>> characteristic = floor(x)
   characteristic = 1
>> mantissa = x - characteristic
   mantissa = 0.0986

>> % Now do a negative-log example
>> x = log(0.05)
   x = -2.9957
>> characteristic = floor(x)
   characteristic = -3
>> mantissa = x - characteristic
   mantissa = 0.0043

Logarithms were used in the days before computers to perform multiplication of large numbers. Since $ \log(xy) = \log(x)+\log(y)$, one can look up the logs of $ x$ and $ y$ in tables of logarithms, add them together (which is easier than multiplying), and look up the antilog of the result to obtain the product $ xy$. Log tables are still used in modern computing environments to replace expensive multiplies with less-expensive table lookups and additions. This is a classic trade-off between memory (for the log tables) and computation. Nowadays, large numbers are multiplied using FFT fast-convolution techniques.

Changing the Base

By definition, $ x = b^{\log_b(x)}$. Taking the log base $ a$ of both sides gives

$\displaystyle \log_a(x) = \log_b(x) \log_a(b) $

which tells how to convert the base from $ b$ to $ a$, that is, how to convert the log base $ b$ of $ x$ to the log base $ a$ of $ x$. (Just multiply by the log base $ a$ of $ b$.)

Logarithms of Negative and Imaginary Numbers

By Euler's identity, $ e^{j\pi} = -1$, so that

$\displaystyle \ln(-1) = j\pi $

from which it follows that for any $ x<0$, $ \ln(x) = j\pi + \ln(\vert x\vert)$.

Similarly, $ e^{j\pi/2} = j$, so that

$\displaystyle \ln(j) = j\frac{\pi}{2} $

and for any imaginary number $ z = jy$, $ \ln(z) = j\pi/2 + \ln(y)$, where $ y$ is real.

Finally, from the polar representation $ z=r e^{j\theta}$ for complex numbers,

$\displaystyle \ln(z) \isdef \ln(r e^{j\theta}) = \ln(r) + j\theta $

where $ r>0$ and $ \theta$ are real. Thus, the log of the magnitude of a complex number behaves like the log of any positive real number, while the log of its phase term $ e^{j\theta }$ extracts its phase (times $ j$).

Decibels

A decibel (abbreviated dB) is defined as one tenth of a bel. The belF.1 is an amplitude unit defined for sound as the log (base 10) of the intensity relative to some reference intensity,F.2 i.e.,

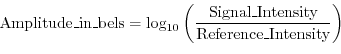
\begin{displaymath} \mbox{Amplitude\_in\_bels} = \log_{10}\left(\frac{\mbox{Signal\_Intensity}}{\mbox{Reference\_Intensity}}\right) \end{displaymath}

The choice of reference intensity (or power) defines the particular choice of dB scale. Signal intensity, power, and energy are always proportional to the square of the signal amplitude. Thus, we can always translate these energy-related measures into squared amplitude:

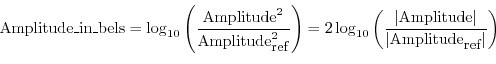
\begin{displaymath} \mbox{Amplitude\_in\_bels} = \log_{10}\left(\frac{\mbox{Amp... ...ft\vert\mbox{Amplitude}_{\mbox{\small ref}}\right\vert}\right) \end{displaymath}

Since there are 10 decibels to a bel, we also have

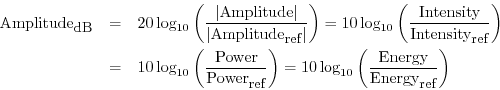
\begin{eqnarray*} \mbox{Amplitude}_{\mbox{\small dB}} &=& 20\log_{10}\left(\fra... ...t(\frac{\mbox{Energy}}{\mbox{Energy}_{\mbox{\small ref}}}\right) \end{eqnarray*}

A just-noticeable difference (JND) in amplitude level is on the order of a quarter dB. In the early days of telephony, one dB was considered a reasonable ``smallest step'' in amplitude, but in reality, a series of half-dB amplitude steps does not sound very smooth, while quarter-dB steps do sound pretty smooth. A typical professional audio filter-design specification for ``ripple in the passband'' is 0.1 dB.

Properties of DB Scales

In every kind of dB, a factor of 10 in amplitude increase corresponds to a 20 dB boost (increase by 20 dB):

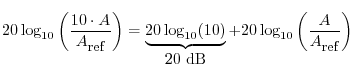
$\displaystyle 20\log_{10}\left(\frac{10 \cdot A}{A_{\mbox{\small ref}}}\right) ... ...)}_{\mbox{$20$\ dB}} + 20\log_{10}\left(\frac{A}{A_{\mbox{\small ref}}}\right) $

and $ 20\log_{10}(10) = 20$, of course. A function $ f(x)$ which is proportional to $ 1/x$ is said to ``fall off'' (or ``roll off'') at the rate of $ 20$ dB per decade. That is, for every factor of $ 10$ in $ x$ (every ``decade''), the amplitude drops $ 20$ dB.

Similarly, a factor of 2 in amplitude gain corresponds to a 6 dB boost:

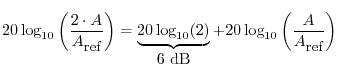
$\displaystyle 20\log_{10}\left(\frac{2 \cdot A}{A_{\mbox{\small ref}}}\right) =... ...2)}_{\mbox{$6$\ dB}} + 20\log_{10}\left(\frac{A}{A_{\mbox{\small ref}}}\right) $

and

$\displaystyle 20\log_{10}(2) = 6.0205999\ldots \approx 6 \;$   dB$\displaystyle . \protect$

A function $ f(x)$ which is proportional to $ 1/x$ is said to fall off $ 6$ dB per octave. That is, for every factor of $ 2$ in $ x$ (every ``octave''), the amplitude drops close to $ 6$ dB. Thus, 6 dB per octave is the same thing as 20 dB per decade.

A doubling of power corresponds to a 3 dB boost:

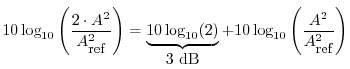
$\displaystyle 10\log_{10}\left(\frac{2 \cdot A^2}{A^2_{\mbox{\small ref}}}\righ... ...{\mbox{$3$\ dB}} + 10\log_{10}\left(\frac{A^2}{A^2_{\mbox{\small ref}}}\right) $

and

$\displaystyle 10\log_{10}(2) = 3.010\ldots \approx 3\;$dB$\displaystyle . \protect$

Finally, note that the choice of reference merely determines a vertical offset in the dB scale:

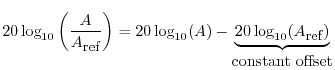
$\displaystyle 20\log_{10}\left(\frac{A}{A_{\mbox{\small ref}}}\right) = 20\log_... ...(A) - \underbrace{20\log_{10}(A_{\mbox{\small ref}})}_{\mbox{constant offset}} $

Specific DB Scales

Since we so often rescale our signals to suit various needs (avoiding overflow, reducing quantization noise, making a nicer plot, etc.), there seems to be little point in worrying about what the dB reference is--we simply choose it implicitly when we rescale to obtain signal values in the range we want to see. In particular, dB relative to full scale ( $ 20\log_{10}(A/A_{\mbox{\small max}})$), abbreviated dBFS, is perhaps the most commonly used case in the digital audio world. Thus, 0 dBFS means maximum amplitude, and typical amplitude levels are negative in dBFS. In addition, there are a few specific dB scales that are worth knowing about.

DBm Scale

One common dB scale in audio recording is the dBm scale in which the reference power is taken to be a milliwatt (1 mW) dissipated by a 600 Ohm resistor. (See §F.3 for a primer on resistors, voltage, current, and power.)

DBV Scale

Another dB scale is the dBV scale which sets 0 dBV to 1 volt. Thus, a 100-volt signal is

$\displaystyle 20\log_{10}\left(\frac{100V}{1V}\right) =$   40 dBV

and a 1000-volt signal is

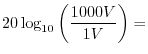$\displaystyle 20\log_{10}\left(\frac{1000V}{1V}\right) =$   60 dBV

Note that the dBV scale is undefined for current or power, unless the voltage is assumed to be across a standard resistor value, such as 600 Ohms.

DB SPL

Sound Pressure Level (SPL) is defined using a reference which is approximately the intensity of 1000 Hz sinusoid that is just barely audible (zero ``phons''). In pressure units:F.3

\begin{eqnarray*} \mbox{$0$\ dB SPL} &\isdef & \mbox{0.0002 $\mu$bar (micro-baro... ...c{\mbox{\small nt}}{\mbox{\small m}^2} \quad\mbox{(MKS units)} \end{eqnarray*}

In intensity units:

$\displaystyle I_0 = 10^{-16} \frac{\mbox{\small W}}{\mbox{\small cm}^2} $

which corresponds to a root-mean-square (rms) pressure amplitude of $ 20.4$ $ \mu$Pa, or about $ 20$ $ \mu$Pa, as listed above. The wave impedance of air plays the role of ``resistor'' in relating the pressure- and intensity-based references exactly analogous to the dBm case discussed above.

Since sound is created by a time-varying pressure, we compute sound levels in dB-SPL by using the average intensity (averaged over at least one period of the lowest frequency contained in the sound).

Table F.1 gives a list of common sound levels and their dB equivalents [54]:

Table F.1: Approximate dB-SPL level of common sounds. (Information from S. S. Stevens, F. Warshofsky, and the Editors of Time-Life Books, Sound and Hearing, Life Science Library, Time-Life Books, Alexandria, VA, 1965, p. 173.)
Sound dB-SPL
Jet engine at 3m 140
Threshold of pain 130
Rock concert 120
Accelerating motorcycle at 5m 110
Pneumatic hammer at 2m 100
Noisy factory 90
Vacuum cleaner 80
Busy traffic 70
Quiet restaurant 50
Residential area at night 40
Empty movie house 30
Rustling of leaves 20
Human breathing (at 3m) 10
Threshold of hearing (good ears) 0


In my experience, the ``threshold of pain'' is most often defined as 120 dB.

The relationship between sound amplitude and actual loudness is complex [76]. Loudness is a perceptual dimension while sound amplitude is physical. Since loudness sensitivity is closer to logarithmic than linear in amplitude (especially at moderate to high loudnesses), we typically use decibels to represent sound amplitude, especially in spectral displays.

The sone amplitude scale is defined in terms of actual loudness perception experiments [76]. At 1kHz and above, loudness perception is approximately logarithmic above 50 dB SPL or so. Below that, it tends toward being more linear.

The phon amplitude scale is simply the dB scale at 1kHz [76, p. 111]. At other frequencies, the amplitude in phons is defined by following the equal-loudness curve over to 1 kHz and reading off the level there in dB SPL. In other words, all pure tones have the same loudness at the same phon level, and 1 kHz is used to set the reference in dB SPL. Just remember that one phon is one dB-SPL at 1 kHz. Looking at the Fletcher-Munson equal-loudness curves [76, p. 124], loudness in phons can be read off along the vertical line at 1 kHz.

Classically, the intensity level of a sound wave is its dB SPL level, measuring the peak time-domain pressure-wave amplitude relative to $ 10^{-16}$ watts per centimeter squared (i.e., there is no consideration of the frequency domain here at all).

Another classical term still encountered is the sensation level of pure tones: The sensation level is the number of dB SPL above the hearing threshold at that frequency [76, p. 110].

For further information on ``doing it right,'' see, for example,
http://www.measure.demon.co.uk/Acoustics_Software/loudness.html.

DBA (A-Weighted DB)

The so-called A-weighted dB scale (abbreviated dBA) is based on the Fletcher-Munson equal-loudness curve for an SPL of 40 phons.F.4 Thus, a dBA weighting assumes a fairly quiet pure tone. Despite this assumption, the dBA weighting is often used as an approximate equal loudness adjustment for measured spectra.

An analog filter transfer function that can be used to implement an approximate A-weighting is given byF.5

$\displaystyle H_A(s) = \frac{k_A \cdot s^4}{(s+129.4)^2 (s+676.7) (s+4636) (s+76655)^2} $

where $ k_A \approx 7.39705\times 10^9$ normalizes the gain to unity at 1 kHz.

The ITU-R 468 noise weightingF.6is said to perform better for measuring noise in audio systems.

DB for Display

In practical signal processing, it is common to choose the maximum signal magnitude as the reference amplitude. That is, we normalize the signal so that the maximum amplitude is defined as 1, or 0 dB. This convention is also used by ``sound level meters'' in audio recording. When displaying magnitude spectra, the highest spectral peak is often normalized to 0 dB. We can then easily read off lower peaks as so many dB below the highest peak.

Figure F.1b shows a plot of the Fast Fourier Transform (FFT) of ten periods of a ``Kaiser-windowed'' sinusoid at $ 440$ Hz. (FFT windows are introduced in §8.1.4. The window is used to taper a finite-duration section of the signal.) Note that the peak dB magnitude has been normalized to zero, and that the plot has been clipped at -100 dB.

Figure F.1: Windowed sinusoid (top) and its FFT magnitude (bottom).
\includegraphics[width=\twidth]{eps/freqdpy}

Below is the Matlab code for producing Fig.F.1. Note that it contains several elements (windows, zero padding, spectral interpolation) that we will not cover until later. They are included here as ``forward references'' in order to keep the example realistic and practical, and to give you an idea of ``how far we have to go'' before we know how to do practical spectrum analysis. Otherwise, the example just illustrates plotting spectra on an arbitrary dB scale between convenient limits. 

% Practical display of the fft of a synthesized sinusoid

fs = 44100;             % Sampling rate
f = 440;                % Sinusoidal frequency = A-440
nper = 10;              % Number of periods to synthesize
dur = nper/f;           % Duration in seconds
T = 1/fs;               % Sampling period
t = 0:T:dur;            % Discrete-time axis in seconds
L = length(t)           % Number of samples to synthesize
ZP = 5;                 % Zero padding factor
N = 2^(nextpow2(L*ZP))  % FFT size (power of 2)

x = cos(2*pi*f*t);      % A sinusoid at A-440 ("row vector")
w = kaiser(L,8);        % An "FFT window"
xw = x .* w';           % Need to transpose w to get a row
sound(xw,fs);           % Might as well listen to it
xzp = [xw,zeros(1,N-L)];% Zero-padded FFT input buffer
X = fft(xzp);           % Interpolated spectrum of xw

Xmag = abs(X);          % Spectral magnitude
Xdb = 20*log10(Xmag);   % Spectral magnitude in dB

XdbMax = max(Xdb);      % Peak dB magnitude
Xdbn = Xdb - XdbMax;    % Normalize to 0dB peak

dBmin = -100;           % Don't show anything lower than this
Xdbp = max(Xdbn,dBmin); % Normalized, clipped, dB mag spec
fmaxp = 2*f;            % Upper frequency limit of plot, Hz
kmaxp = fmaxp*N/fs;     % Upper frequency limit of plot, bins
fp = fs*[0:kmaxp]/N;    % Frequency axis in Hz

% Ok, plot it already!

subplot(2,1,1);
plot(1000*t,xw);
xlabel('Time (ms)');
ylabel('Amplitude');
title(sprintf(['a) %d Periods of a %3.0f Hz Sinusoid, ',
               'Kaiser Windowed'],nper,f)R);

subplot(2,1,2);
plot(fp,Xdbp(1:kmaxp+1)); grid;
% Plot a dashed line where the peak should be:
  hold on; plot([440 440],[dBmin,0],'--'); hold off;
xlabel('Frequency (Hz)');
ylabel('Magnitude (dB)');
title(sprintf(['b) Interpolated FFT of %d Periods of ',...
        '%3.0f Hz Sinusoid'],nper,f));

The following more compact Matlab produces essentially the same plot, but without the nice physical units on the horizontal axes: 

x = cos([0:2*pi/20:10*2*pi]); % 10 periods, 20 samples/cycle
L = length(x);
xw = x' .* kaiser(L,8);
N = 2^nextpow2(L*5);
X = fft([xw',zeros(1,N-L)]);

subplot(2,1,1); plot(xw);
xlabel('Time (samples)'); ylabel('Amplitude');
title('a) 10 Periods of a Kaiser-Windowed Sinusoid');

subplot(2,1,2); kmaxp = 2*10*5; Xl = 20*log10(abs(X(1:kmaxp+1)));
plot([10*5+1,10*5+1],[-100,0],[0:kmaxp],max(Xl-max(Xl),-100)); grid;
xlabel('Frequency (Bins)'); ylabel('Magnitude (dB)');
title('b) Interpolated FFT of 10 Periods of Sinusoid');

Dynamic Range

The dynamic range of a signal processing system can be defined as the maximum dB level sustainable without overflow (or other distortion) minus the dB level of the ``noise floor''.

Similarly, the dynamic range of a signal can be defined as its maximum decibel level minus its average ``noise level'' in dB. For digital signals, the limiting noise is ideally quantization noise.

Quantization noise is generally modeled as a uniform random variable between plus and minus half the least significant bit (since rounding to the nearest representable sample value is normally used). If $ q$ denotes the quantization interval, then the maximum quantization-error magnitude is $ q/2$, and its variance (``noise power'') is $ \sigma^2_q = q^2/12$ (see §G.3 for a derivation of this value).

The rms level of the quantization noise is therefore $ \sigma_q = q/(2\sqrt{3})\approx 0.3 q$, or about 60% of the maximum error.

The number system (see Appendix G and number of bits chosen to represent signal samples determines their available dynamic range. Signal processing operations such as digital filtering may use the same number system as the input signal, or they may use extra bits in the computations, yielding an increased ``internal dynamic range''.

Since the threshold of hearing is near 0 dB SPL, and since the ``threshold of pain'' is often defined as 120 dB SPL, we may say that the dynamic range of human hearing is approximately 120 dB.

The dynamic range of magnetic tape is approximately 55 dB. To increase the dynamic range available for analog recording on magnetic tape, companding is often used. ``Dolby A'' adds approximately 10 dB to the dynamic range that will fit on magnetic tape (by compressing the signal dynamic range by 10 dB), while DBX adds 30 dB (at the cost of more ``transient distortion'').F.7 In general, any dynamic range can be mapped to any other dynamic range, subject only to noise limitations.

Voltage, Current, and Resistance

The state of an ideal resistor is completely specified by the voltage across it (call it $ V$ volts) and the current passing through it ($ I$ amperes, or simply ``amps''). The ratio of voltage to current gives the value of the resistor ($ V/I = R = $ resistance in Ohms). The fundamental relation between voltage and current in a resistor is called Ohm's Law:

$\displaystyle V(t) = R \cdot I(t)$   (Ohm's Law)

where we have indicated also that the voltage and current may vary with time (while the resistor value normally does not).

The electrical power in watts dissipated by a resistor R is given by

$\displaystyle {\cal P}= V\cdot I = \frac{V^2}{R} = R\cdot I^2 $

where $ V$ is the voltage and $ I$ is the current. Thus, volts times amps gives watts. Also, volts squared over ohms equals watts, and so on.

Exercises

  1. Show that

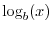    $\displaystyle \frac{d}{dx}\log_b(x) = \frac{1}{x\ln(b)} $

    where $ \log_b(x)$ denotes the logarithm to the base 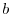$ b$ of $ x$.

  2. Work out the definition of logarithms using a complex base $ b$.

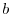  3. Try synthesizing a sawtooth waveform which increases by 1/2 dB a few times per second, and again using 1/4 dB increments. See if you agree that quarter-dB increments are ``smooth'' enough for you.

Next Section:
Number Systems for Digital Audio
Previous Section:
Taylor Series Expansions