Free Books    Physical Audio Signal Processing  

Feedback Comb Filter Amplitude Response

Figure 2.26 shows a family of feedback-comb-filter amplitude responses, obtained using a selection of feedback coefficients.

Figure: Amplitude response of the feedback comb-filter $ H(z) = 1/(1-g z^{-M})$ (Fig.2.24 with $ b_0=1$ and $ -a_M=g$) with $ M=5$ and $ g=0.1$, $ 0.5$, and $ 0.9$. a) Linear amplitude scale. b) Decibel scale.
\includegraphics[width=\twidth ]{eps/fbcfar}

Figure 2.27 shows a similar family obtained using negated feedback coefficients; the opposite sign of the feedback exchanges the peaks and valleys in the amplitude response.

Figure: Amplitude response of the phase-inverted feedback comb-filter, i.e., as in Fig.2.26 with negated $ g=-0.1$, $ -0.5$, and $ -0.9$. a) Linear amplitude scale. b) Decibel scale.
\includegraphics[width=\twidth ]{eps/fbcfiar}

As introduced in §2.6.2 above, a class of feedback comb filters can be defined as any difference equation of the form

$\displaystyle y(n) = x(n) + g\,y(n-M). $

Taking the z transform of both sides and solving for $ H(z)\isdef Y(z)/X(z)$, the transfer function of the feedback comb filter is found to be

$\displaystyle H(z) = \frac{1}{1-g\,z^{-M}}, \protect$ (3.5)

so that the amplitude response is

$\displaystyle G(\omega) \isdef \left\vert H(e^{j\omega})\right\vert = \frac{1}{\left\vert 1 - g e^{-j\omega M}\right\vert}, \quad -\pi \leq \omega \leq \pi . $

This is plotted in Fig.2.26 for $ M=5$ and $ g=0.1$, $ 0.5$, and $ 0.9$. Figure 2.27 shows the same case but with the feedback sign-inverted.

For $ g=1$, the feedback-comb amplitude response reduces to

$\displaystyle G(\omega) = \frac{1}{2\left\vert\sin(\omega M/2)\right\vert}, $

and for $ g=-1$ to

$\displaystyle G(\omega) = \frac{1}{2\left\vert\cos(\omega M/2)\right\vert}, $

which exactly inverts the amplitude response of the feedforward comb filter with gain $ g=1$ (Eq.$ \,$(2.4)).

Note that $ g>0$ produces resonant peaks at

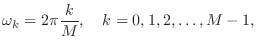
$\displaystyle \omega_k = 2\pi\frac{k}{M}, \quad k=0,1,2,\dots,M-1, $

while for $ g<0$, the peaks occur midway between these values.

Next Section:
Filtered-Feedback Comb Filters
Previous Section:
Feedforward Comb Filter Amplitude Response