DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Freeverb Allpass Approximation

In Eq.$ \,$(3.2) we defined the allpass notation $ \hbox{AP}_{N}^{\,g}$ by

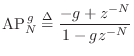
$\displaystyle \hbox{AP}_{N}^{\,g} \isdef \frac{-g + z^{-N}}{1 - g z^{-N}} $

A look at allpass.h reveals that Freeverb implements

$\displaystyle \hbox{AP}_{N}^{\,g} \approx \frac{-1 + (1+g)z^{-N}}{1 - g z^{-N}}. $

As a result, each of the four Freeverb ``allpass'' sections is really a feedback comb-filter $ \hbox{FBCF}_{N}^{\,g}$ in series with a feedforward comb-filter $ \hbox{FFCF}_{N}^{\,-1,1+g}$, where (cf. §2.6)

\begin{eqnarray*} \hbox{FBCF}_{N}^{\,g} &\isdef & \frac{1}{1 - g\,z^{-N}}\\ [5pt] \hbox{FFCF}_{N}^{\,-1,1+g} &\isdef & -1 + (1+g)z^{-N}. \end{eqnarray*}

A true allpass is obtained only for $ g=(\sqrt{5}-1)/2\approx 0.618$ (reciprocal of the ``golden ratio''). The default value used in Freeverb (see revmodel.cpp) is $ 0.5$. A detailed discussion of feedforward and feedback comb filters appears in §2.6, and corresponding Schroeder allpass filters are described in §2.8.

Next Section:
Conclusions
Previous Section:
Lowpass-Feedback Comb Filter