Lowpass-Feedback Comb Filter
Inspection of comb.h in the Freeverb source shows that Freeverb's ``comb'' filter is more specifically a lowpass-feedback-comb filter (LBCF4.11--§2.6.5). It is constructed using a delay line whose output is lowpass-filtered and summed with the delay-line's input. The particular lowpass used in Freeverb is a unity-gain one-pole lowpass having the transfer function
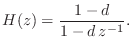
In Freeverb's comb section (comb.h and
comb.cpp), the ``damping'' ![]() is set initially to
is set initially to
Increasing the roomsize parameter (typically brought out to a
GUI slider) increases ![]() and hence the reverberation time. Since
and hence the reverberation time. Since
![]() is required for dc stability, the roomsize must be less
than 1.0714, and so the GUI slider max is typically 1 (
is required for dc stability, the roomsize must be less
than 1.0714, and so the GUI slider max is typically 1 (![]() ).
).
The feedback variable ![]() mainly determines reverberation
time at low-frequencies at which the feedback lowpass has negligible
effect. The feedback lowpass causes the reverberation time to
decrease with frequency, which is natural. At very high
frequencies--those for which the lowpass gain times
mainly determines reverberation
time at low-frequencies at which the feedback lowpass has negligible
effect. The feedback lowpass causes the reverberation time to
decrease with frequency, which is natural. At very high
frequencies--those for which the lowpass gain times ![]() is much less
than 0.5--the reverberation time becomes dominated by the diffusion
allpass filters (which have a fixed feedback coefficient of
is much less
than 0.5--the reverberation time becomes dominated by the diffusion
allpass filters (which have a fixed feedback coefficient of ![]() ).
Thus, in Freeverb, the ``room size'' parameter can be interpreted as
setting the low-frequency T60 (time to decay 60 dB), while the
``damping'' parameter controls how rapidly T60 shortens as a function
of increasing frequency. A lower-limit on T60 is given by the four
diffusion allpass filters.
).
Thus, in Freeverb, the ``room size'' parameter can be interpreted as
setting the low-frequency T60 (time to decay 60 dB), while the
``damping'' parameter controls how rapidly T60 shortens as a function
of increasing frequency. A lower-limit on T60 is given by the four
diffusion allpass filters.
In terms of the physical interpretation of the filtered-feedback comb-filter discussed in §2.6.5, Freeverb's roomsize parameter can be interpreted as the square-root of the low-frequency reflection-coefficient of each wall. That is, when a planewave bounces back and forth between two walls, the attenuation coefficient is roomsize after one round trip (two wall reflections). Therefore, a better name in this interpretation would be liveness or reflectivity. Since the round-trip delay is given in samples by the delay-line length, changing the roomsize requires changing the delay-line lengths in this interpretation.
Next Section:
Freeverb Allpass Approximation
Previous Section:
Freeverb Main Loop



















