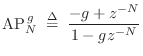Schroeder Reverberators
The subject of artificial reverberation was initiated in the early 1960s by Manfred Schroeder [417,412]. Early Schroeder reverberators consisted of the following elements [412]:
- A series connection of several allpass filters
- A parallel bank of feedback comb filters
- A mixing matrix
![\includegraphics[width=\twidth]{eps/jcrevmus10}](http://www.dsprelated.com/josimages_new/pasp/img706.png) |
An example is shown in Fig.3.5, where, in that figure,
denotes a Schroeder allpass section with delay length
denotes a feedback comb filter with delay length
![$\displaystyle \eqsp \left[\begin{array}{rrrr}
1 & 1 & 1 & 1 \\ [2pt]
-1 & -1 & -1 & -1 \\ [2pt]
-1 & 1 & -1 & 1 \\ [2pt]
1 & -1 & 1 & -1
\end{array}\right]
$](http://www.dsprelated.com/josimages_new/pasp/img709.png)
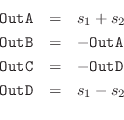
|

|
As discussed above in §3.4.2, the allpass filters provide ``colorless'' high-density echoes in the late impulse response of the reverberator [417]. These allpass filters may also be referred to as diffusers. While allpass filters are ``colorless'' in theory, perceptually, their impulse responses are only colorless when they are extremely short (less than 10 ms or so). Longer allpass impulse responses sound similar to feedback comb-filters. For steady-state tones, however, such as sinusoids, the allpass property gives the same gain at every frequency, unlike comb filters.
Schroeder [412, p. 221] suggests a progression of allpass delay-line lengths close to
The parallel comb-filter bank is intended to give a psychoacoustically appropriate fluctuation in the reverberator frequency response. As discussed in Chapter 2 (§2.6.2), a feedback comb filter can simulate a pair of parallel walls, so one could choose the delay-line length in each comb filter to be the number of samples it takes for a plane wave to propagate from one wall to the opposite wall and back. However, in his original paper [412], Schroeder describes a more psychoacoustically motivated approach:
``There are about 15 large response peaks in every 100 cps [Hz] interval for a room with 1 sec reverberation time. Thus, one might hope that if an artificial reverberator has a comparable number of response peaks it might sound just as good as a real room. We have been able to confirm this expectation by subjective evaluations of the responses of reverberators consisting of several comb filters ... connected in parallel. For a delay of 0.04 sec, the number of response peaks per 100 cps [Hz] is 4. Thus, between 3 and 4 comb filters in parallel ... with incommensurate delays, are required to approximate the number of peaks in the frequency reponse of a room having a reverberation time of T[60] = 1 sec. Also, the open loop gain of the comb filters should not exceed about 0.85 or -1.4 dB to keep the response fluctuations from being excessive.''Thus, one may choose the comb-filter delay-line lengths more or less arbitrarily, and then use enough of them in parallel (with mutually prime delay-line lengths) to achieve a perceptually adequate fluctuation density in the frequency-response magnitude. In [412], four such delays are chosen between 30 and 45 ms, and the corresponding feedback coefficients
The delay lengths shown in Fig.3.7 were optimized by ear by John
Chowning (and perhaps others at CCRMA) for an audio sampling rate of
![]() kHz.
kHz.
Finally, for multichannel listening, Schroeder suggested [412] a mixing matrix at the reverberator output. The goal of the mixing matrix is to bring out any number of uncorrelated audio channels of reverberation (for any number of output speakers) [153, p. 111-112].
Example Schroeder Reverberators
Additional example Schroeder Reverberators, drawn from CCRMA software listings, are shown in Figures 3.6 and 3.7. The notation used in the figures is explained above in Equations (3.2-3.3).
![\includegraphics[width=\twidth]{eps/satrev}](http://www.dsprelated.com/josimages_new/pasp/img719.png) |
![\includegraphics[width=\twidth]{eps/jcrev}](http://www.dsprelated.com/josimages_new/pasp/img720.png) |
A software musical instrument using one of these reverberators simply adds its output, suitably scaled, to the real-time variable RevIn (the global reverberator input sample at the current time). In both examples, we again see three Schroeder allpass filters in series (Schroeder suggested five, as disussed above).
The rather small reverberator of Fig.3.6 is thought to have been used in John Chowning's often-heard FM-brass canon sound examples.4.8Like the more computationally expensive four-channel-audio example in Fig.3.5, it is designed for a 25 kHz sampling rate. Its ``mixing matrix'' is simply a negation of the right stereo channel.
In addition to the allpass chain in Figures 3.6 and 3.7, there is a parallel bank of four feedback comb filters. Since all of the filters are linear and time-invariant [449], the series allpass chain can go either before or after the parallel comb-filter bank. Unlike the allpass filters, the comb filters have an irregular magnitude frequency response, and they can be considered a simulation of four specific echo sequences. The delay lengths in these comb filters may be used to adjust the illusion of ``room size'', although if they are shortened, there should be more of them in parallel, according to Schroeder's quote above.
In Fig.3.7, the reverbator output signal RevOut is fed
to the four audio output channels via four delay lines. These delay
lengths are specified relative to the sampling rate ![]() .4.9 Output delay lines can substitute for or supplement
a mixing matrix as a means for decorrelating the reverberation
output channels (to minimize reverberation imaging between
speakers). In this particular case, however, the delays are evidently
not optimized for decorrelation. Also, for purposes of decorrelation,
the shortest delay can be subtracted from the other three and its
corresponding delay-line eliminated.
.4.9 Output delay lines can substitute for or supplement
a mixing matrix as a means for decorrelating the reverberation
output channels (to minimize reverberation imaging between
speakers). In this particular case, however, the delays are evidently
not optimized for decorrelation. Also, for purposes of decorrelation,
the shortest delay can be subtracted from the other three and its
corresponding delay-line eliminated.
A Schroeder reverberator along the above lines may be found in the Synthesis Tool Kit (STK) [86]. See files JCRev.cpp and JCRev.h.
The reverberators shown in Figures 3.5 and 3.6 above are included in the Faust distribution. See functions jcrev, satrev, and reverb_demo in the effect.lib library. While these Schroeder reverberators are quite small by today's standards, they are well tuned for their size. More commonly used today is freeverb (included in the examples directory of the Faust distribution as freeverb.dsp), discussed next.
Next Section:
Freeverb
Previous Section:
Late Reverberation Approximations