DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Frequency-Dependent Damping

In real vibrating strings, damping typically increases with frequency for a variety of physical reasons [73,77]. A simple modification [392] to Eq.$ \,$(6.14) yielding frequency-dependent damping is

$\displaystyle Ky''= \epsilon {\ddot y}+ \mu{\dot y}+ \mu_2{\dot y''}. $

See §C.5.2 for some analysis of damped PDEs of this nature. A book-chapter by Vallette containing a thorough analysis of damped vibrating strings is given in [517].

The result of adding such damping terms to the wave equation is that traveling waves on the string decay at frequency-dependent rates. This means the loss factors $ g$ of the previous section should really be digital filters having gains which decrease with frequency (and never exceed $ 1$ for stability of the loop). These filters commute with delay elements because they are linear and time invariant (LTI) [449]. Thus, following the reasoning of the previous section, they can be lumped at a single point in the digital waveguide. Let $ {\hat G}(z)$ denote the resulting string loop filter (replacing $ g^N$ in Fig.6.127.7). We have the stability (passivity) constraint $ \vert{\hat G}(e^{j\omega T})\vert\leq1$, and making the filter linear phase (constant delay at all frequencies) will restrict consideration to symmetric FIR filters only.

Restriction to FIR filters yields the important advantage of keeping the approximation problem convex in the weighted least-squares norm. Convexity of a norm means that gradient-based search techniques can be used to find a global miminizer of the error norm without exhaustive search [64],[428, Appendix A].

The linear-phase requirement halves the degrees of freedom in the filter coefficients. That is, given $ {\hat g}(n)$ for $ n\geq0$, the coefficients $ {\hat g}(-n)={\hat g}(n)$ are also determined. The loss-filter frequency response can be written in terms of its (impulse response) coefficients as

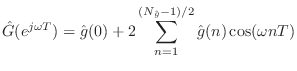
$\displaystyle {\hat G}(e^{j\omega T}) = {\hat g}(0) + 2\sum_{n=1}^{(N_{\hat g}-1)/2} {\hat g}(n) \cos(\omega n T) $

where $ \omega T=2\pi f T=2\pi f/f_s$, and the impulse-response length $ N_{\hat g}$ is assumed odd.

A further degree of freedom is eliminated from the loss-filter approximation by assuming all losses are insignificant at 0 Hz so that $ G(0)=1\,\,\Rightarrow\,\,{\hat G}(1)=1$ (taking the approximation error to be zero at $ \omega=0$). This means the coefficients of the FIR filter must sum to $ 1$. If the length of the filter is $ N_{\hat g}$, we have

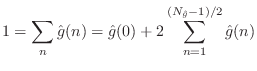
$\displaystyle 1 = \sum_n {\hat g}(n) = {\hat g}(0) + 2\sum_{n=1}^{(N_{\hat g}-1)/2} {\hat g}(n) $

Next Section:
The Stiff String
Previous Section:
The Damped Plucked String