Free Books
   Free Books    Physical Audio Signal Processing  

The Stiff String

Stiffness in a vibrating string introduces a restoring force proportional to the bending angle of the string. As discussed further in §C.6, the usual stiffness term added to the wave equation for the ideal string yields

$\displaystyle \epsilon {\ddot y}= Ky''- \kappa y''''. $

When this wave equation is solved in terms of traveling waves (§C.6), it emerges that high-frequency wave components travel faster than low-frequency components. In other words, wave propagation in stiff strings is dispersive. (See §C.6 for details.)

Stiff-string models are commonly used in piano synthesis. In §9.4, further details of string models used in piano synthesis are described (§9.4.1).

Experiments with modified recordings of acoustic classical guitars indicate that overtone inharmonicity due to string-stiffness is generally not audible in nylon-string guitars, although just-noticeable-differences are possible for the 6th (lowest) string [225]. Such experiments may be carried out by retuning the partial overtones in a recorded sound sample so that they become exact harmonics. Such retuning is straightforward using sinusoidal modeling techniques [359,456].

Stiff String Synthesis Models

Figure 6.13: Commuted simulation of a rigidly terminated, stiff string (no damping).
\includegraphics[width=\twidth]{eps/flstifftstring}

An ideal stiff-string synthesis model is drawn in Fig. 6.13 [10]. See §C.6 for a detailed derivation. The delay-line length $ N$ is the number of samples in $ K$ periods at frequency $ f_K$, where $ K$ is the number of the highest partial supported (normally the last one before $ f_s/2$). This is the counterpart of Fig. 6.12 which depicted ideal-string damping which was lumped at a single point in the delay-line loop. For the ideal stiff string, however, (no damping), it is dispersion filtering that is lumped at a single point of the loop. Dispersion can be lumped like damping because it, too, is a linear, time-invariant (LTI) filtering of a propagating wave. Because it is LTI, dispersion-filtering commutes with other LTI systems in series, such as delay elements. The allpass filter in Fig.C.9 corresponds to filter $ H_s(z)$ in Fig.9.2 for the Extended Karplus-Strong algorithm. In practice, losses are also included for realistic string behavior (filter $ H_d(z)$ in Fig.9.2).

Allpass filters were introduced in §2.8, and a fairly comprehensive summary is given in Book II of this series [449, Appendix C].7.8The general transfer function for an allpass filter is given (in the real, single-input, single-output case) by

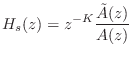
$\displaystyle H_s(z) = z^{-K} \frac{\tilde{A}(z)}{A(z)} $

where $ K\geq 0$ is an integer pure-delay in samples (all delay lines are allpass filters),

$\displaystyle A(z) \isdef 1 + a_1 z^{-1}+ a_2 z^{-2} + \cdots + a_Nz^{-N}, $

and

$\displaystyle \tilde{A}(z)\isdef z^{-N}\overline{A}(z^{-1}) = \overline{a_N} +... ...^{-1}+ \overline{a_{N-2}} z^{-2} + \cdots + \overline{a_1} z^{-N+1} + z^{-N}. $

We may think of $ \tilde{A}(z)$ as the flip of $ A(z)$. For example, if $ A(z)=1+1.4z^{-1}+0.49z^{-2}$, we have $ \tilde{A}(z)=0.49+1.4z^{-1}+z^{-2}$. Thus, $ \tilde{A}(z)$ is obtained from $ A(z)$ by simply reversing the order of the coefficients (and conjugating them if they are complex, but normally they are real in practice). For an allpass filter $ H_s(z)$ simulating stiffness, we would normally have $ K=0$, since the filter is already in series with a delay line.

Section 6.11 below discusses some methods for designing stiffness allpass filters $ H_s(z)$ from measurements of stiff vibrating strings, and §9.4.1 gives further details for the case of piano string modeling.

Next Section:
The Externally Excited String
Previous Section:
Frequency-Dependent Damping