Free Books
   Free Books    Physical Audio Signal Processing  

Fundamental Frequency Estimation

As mentioned in §6.11.2 above, it is advisable to estimate the fundamental frequency of vibration (often called ``F0'') in order that the partial overtones are well resolved while maintaining maximum time resolution for estimating the decay time-constant.

Below is a summary of the F0 estimation method used in calibrating loop filters with good results [471]:

  • Take an FFT of the middle third of a recorded plucked string tone.
  • Find the frequencies and amplitudes of the largest $ K$ peaks, where $ K$ is chosen so that the $ K$ retained peaks all have a reasonable signal-to-noise ratio.
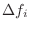
  • Form a histogram of peak spacing $ \Delta f_i$
  • The pitch estimate 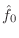$ {\hat f}_0$ is defined as the most common spacing 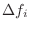$ \Delta f_i$ in the histogram.
The F0 estimate so formed is sufficiently accurate for purposes of calibrating a peak tracker for decay-rate estimation. (The F0 value is only used to set the FFT window length in the STFT to four nominal periods under the window, so it is not critical.)

Approximate Maximum Likelihood F0 Estimation

In applications for which the fundamental frequency F0 must be measured very accurately in a periodic signal, the estimate $ {\hat f}_0$ obtained by the above algorithm can be refined using a gradient search which matches a so-called ``harmonic comb'' to the magnitude spectrum of an interpolated FFT $ X(\omega)$:

$\displaystyle {\hat f}_0 \isdefs \arg\max_{{\hat f}_0} \sum_{k=1}^K \log\left[\... ...f}_0} \prod_{k=1}^K \left[\left\vert X(k{\hat f}_0)\right\vert+\epsilon\right] $

where

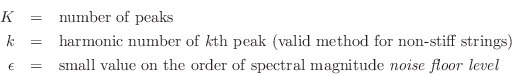
\begin{eqnarray*} K &=& \mbox{number of peaks}\\ k &=& \mbox{harmonic number of... ...lue on the order of spectral magnitude \emph{noise floor level}} \end{eqnarray*}

Note that freely vibrating strings are not exactly periodic due to exponenential decay, coupling effects, and stiffness (which stretches harmonics into quasiharmonic overtones, as explained in §6.9). However, non-stiff strings can often be analyzed as having approximately harmonic spectra ( $ \leftrightarrow$ periodic time waveform) over a limited time frame.

Since string spectra typically exhibit harmonically spaced nulls associated with the excitation and/or observation points, as well as from other phenomena such as recording multipath and/or reverberation, it is advisable to restrict $ K$ to a range that does not include any spectral nulls (or simply omit index $ k$ when $ k{\hat f}_0$ is too close to a spectral null), since even one spectral null can push the product of peak amplitudes to a very small value. As a practical matter, it is important to inspect the magnitude spectra of the data manually to ensure that a robust row of peaks is being matched by the harmonic comb. For example, a display of the frame magnitude spectrum overlaid with vertical lines at the optimized harmonic-comb frequencies yields an effective picture of the F0 estimate in which typical problems (such as octave errors) are readily seen.

References on F0 Estimation

An often-cited book on classical methods for pitch detection, particularly for voice, is that by Hess [192]. The harmonic comb method can be considered an approximate maximum-likelihood pitch estimator, and more accurate maximum-likelihood methods have been worked out [114,547,376,377]. More recently, Klapuri has been developing some promising methods for multiple pitch estimation [254,253,252].7.12A comparison of real-time pitch-tracking algorithms applied to guitar is given in [260], with consideration of latency (time delay).

Extension to Stiff Strings

An advantage of the harmonic-comb method, as well as other frequency-domain maximum-likelihood pitch-estimation methods, is that it is easily extended to accommodate stiff strings. For this, the stretch-factor in the spectral-peak center-frequencies can be estimated--the so-called coefficient of inharmonicity, and then the harmonic-comb (or other maximum-likelihood spectral-matching template) can be stretched by the same amount, so that when set to the correct pitch, the template matches the data spectrum more accurately than if harmonicity is assumed.

Next Section:
EDR-Based Loop-Filter Design
Previous Section:
Dispersion Filter Design