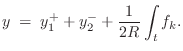Incorporating Control Motion
Let ![]() denote the vertical position of the mass
in Fig.9.22. (We still assume
denote the vertical position of the mass
in Fig.9.22. (We still assume ![]() .) We can think of
.) We can think of
![]() as the position of the control point on the
plectrum, e.g., the position of the ``pinch-point'' holding the
plectrum while plucking the string. In a harpsichord,
as the position of the control point on the
plectrum, e.g., the position of the ``pinch-point'' holding the
plectrum while plucking the string. In a harpsichord, ![]() can be
considered the jack position [347].
can be
considered the jack position [347].
Also denote by ![]() the rest length of the spring
the rest length of the spring ![]() in Fig.9.22, and let
in Fig.9.22, and let
![]() denote the
position of the ``end'' of the spring while not in contact with the
string. Then the plectrum makes contact with the string when
denote the
position of the ``end'' of the spring while not in contact with the
string. Then the plectrum makes contact with the string when
Let the subscripts ![]() and
and ![]() each denote one side of the scattering
system, as indicated in Fig.9.23. Then, for example,
each denote one side of the scattering
system, as indicated in Fig.9.23. Then, for example,
![]() is the displacement of the string on the left (side
is the displacement of the string on the left (side
![]() ) of plucking point, and
) of plucking point, and ![]() is on the right side of
is on the right side of ![]() (but
still located at point
(but
still located at point ![]() ). By continuity of the string, we have
). By continuity of the string, we have
When the spring engages the string (![]() ) and begins to compress,
the upward force on the string at the contact point is given by
) and begins to compress,
the upward force on the string at the contact point is given by
During contact, force equilibrium at the plucking point requires (cf. §9.3.1)
where
Substituting
![]() and taking the Laplace transform yields
and taking the Laplace transform yields
![$\displaystyle Y(s)
\eqsp Y_1^+(s) + Y_2^-(s) + \frac{1}{2R} \frac{F_k(s)}{s}
\eqsp Y_1^+(s) + Y_2^-(s) + \frac{k}{2Rs}\left[Y_e(s) - Y(s)\right].
$](http://www.dsprelated.com/josimages_new/pasp/img2224.png)
![\begin{eqnarray*}
Y(s) &=& \left[1-\hat{\rho}_f(s)\right]\cdot
\left[Y_1^+(s)+Y...
...)\cdot \left\{Y_e(s)
- \left[Y_1^+(s)+Y_2^-(s)\right]\right\},
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img2226.png)
where, as first noted at Eq.![]() (9.24) above,
(9.24) above,

![\begin{eqnarray*}
Y_d^+ &=& Y_e - \left(Y_1^+ + Y_2^-\right)\\ [5pt]
Y_1^- &=& Y...
...\hat{\rho}_f Y_d^+\\ [5pt]
Y_2^+ &=& Y_1^+ + \hat{\rho}_f Y_d^+.
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img2228.png)
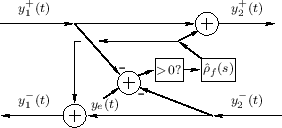
This system is diagrammed in Fig.9.24. The manipulation of the
minus signs relative to Fig.9.23 makes it convenient for
restricting ![]() to positive values only (as shown in the
figure), corresponding to the plectrum engaging the string going up.
This uses the approximation
to positive values only (as shown in the
figure), corresponding to the plectrum engaging the string going up.
This uses the approximation
![]() ,
which is exact when
,
which is exact when
![]() , i.e., when the plectrum does not affect
the string displacement at the current time. It is therefore exact at
the time of collision and also applicable just after release.
Similarly,
, i.e., when the plectrum does not affect
the string displacement at the current time. It is therefore exact at
the time of collision and also applicable just after release.
Similarly,
![]() can be used to trigger a release of the
string from the plectrum.
can be used to trigger a release of the
string from the plectrum.
Next Section:
Successive Pluck Collision Detection
Previous Section:
Digital Waveguide Plucked-String Model