DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Nested Allpass Filters

An interesting property of allpass filters is that they can be nested [412,152,153]. That is, if $ H_1(z)$ and $ H_2(z)$ denote unity-gain allpass transfer functions, then both $ H_1(H_2(z))$ and $ H_2(H_1(z))$ are allpass filters. A proof can be based on the observation that, since $ \vert H_i(e^{j\omega})\vert=1$, $ H_i(z)$ can be viewed as a conformal map [326] which maps the unit circle in the $ z$ plane to itself; therefore, the set of all such maps is closed under functional composition. Nested allpass filters were proposed for use in artificial reverberation by Schroeder [412, p. 222].

An important class of nested allpass filters is obtained by nesting first-order allpass filters of the form

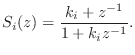
$\displaystyle S_i(z) = \frac{k_i+z^{-1}}{1+k_iz^{-1}}. $

The nesting begins with $ H_1(z)\isdef S_1(z)$, and $ H_2(z)$ is obtained by replacing $ z^{-1}$ in $ H_1(z)$ by $ z^{-1}S_2(z)$ to get

$\displaystyle H_2(z) \isdef S_1\left([z^{-1}S_2(z)]^{-1}\right) \isdef \frac{k_1+z^{-1}S_2(z)}{1+k_1z^{-1}S_2(z)}. $

Figure 2.31a depicts the first-order allpass $ S_1(z)$ in direct form II. Figure 2.31b shows the same filter redrawn as a two-multiplier lattice filter section [297]. In the lattice form, it is clear that replacing $ z^{-1}$ by $ z^{-1}S_2(z)$ just extends the lattice to the right, as shown in Fig.2.32.

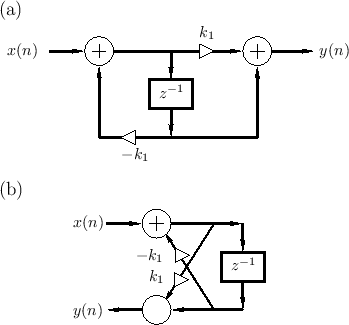
The equivalence of nested allpass filters to lattice filters has computational significance since it is well known that the two-multiply lattice sections can be replaced by one-multiply lattice sections [297,314].

Figure 2.31: First-order allpass filter: (a) Direct form II. (b) Two-multiply lattice section. (b) is just (a) folded over.
\includegraphics{eps/apone}

Figure 2.32: Second-order allpass filter: (a) Nested direct-form II. (b) Consecutive two-multiply lattice sections.
\includegraphics[width=4.45in]{eps/aptwo}

In summary, nested first-order allpass filters are equivalent to lattice filters made of two-multiply lattice sections. In §C.8.4, a one-multiply section is derived which is not only less expensive to implement in hardware, but it additionally has a direct interpretation as a physical model.

Next Section:
More General Allpass Filters
Previous Section:
Allpass from Two Combs