Perceptual Metrics for Ideal Reverberation

Free Books Physical Audio Signal Processing

Some desirable controls for an artificial reverberator include [218]

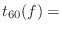$t_{60}(f) =$ desired reverberation time at each frequency
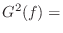signal power gain at each frequency
``clarity'' = ratio of impulse-response energy in early reflections to that in the late reverb
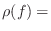$\rho(f) =$ interaural correlation coefficient at left and right ears

The time to decay 60 dB ( $t_{60}$ ) is a classical objective parameter used as a measure of perceived reverberation time. Classically, $t_{60}$ was measured for the whole response. More recently [216], it has become more common to design for a given $t_{60}$ at more than one frequency, e.g., one for low frequencies, another for high frequencies, and interpolated values at intermediate frequencies. Perceptual studies indicate that reverberation time should be independently adjustable in at least three frequency bands [217].

Energy Decay Curve

For measuring and defining reverberation time $t_{60}$ , Schroeder introduced the so-called energy decay curve (EDC) which is the tail integral of the squared impulse response at time :

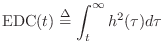
$\displaystyle \hbox{EDC}(t) \isdef \int_t^\infty h^2(\tau)d\tau$

Thus, $\hbox{EDC}(t)$ is the total amount of signal energy remaining in the reverberator impulse response at time

. The EDC decays more smoothly than the impulse response itself, and so it is more useful than ordinary amplitude envelopes for estimating $t_{60}$ .

Energy Decay Relief

The energy decay relief (EDR) is a time-frequency distribution which generalizes the EDC to multiple frequency bands [215]:

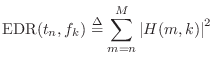
$\displaystyle \hbox{EDR}(t_n,f_k) \isdef \sum_{m=n}^M \left\vert H(m,k)\right\vert^2$

where

denotes bin

of the short-time Fourier transform (STFT) at time-frame

[12,451], and

denotes the total number of time frames. The FFT within the STFT is typically used with a window, such as a Hann window of length 30 or 40 ms.

Thus, $\hbox{EDR}(t_n,f_k)$ is the total amount of signal energy remaining in the reverberator's impulse response at time in a frequency band centered about Hz, where denotes the FFT length.

The EDR of a violin-body impulse response is shown in Fig.3.2. For better correspondence with audio perception, the frequency axis is warped to the Bark frequency scale [459], and energy is summed within each Bark band (one critical band of hearing equals one Bark). A violin body can be regarded as a very small reverberant room, with correspondingly ``magnified'' spectral structure relative to reverberant rooms.

**Figure 3.2:** Energy Decay Relief of a violin-body impulse response (from [203]).
$\includegraphics[width=\twidth]{eps/bodyBEDR}$

The EDR of the Boston Symphony Hall is displayed in [153, p. 96].

The EDR is used to measure partial overtone dampings from recordings of a vibrating string in §6.11.5.

Next Section:
Desired Qualities in Late Reverberation
Previous Section:
Perception of Echo Density and Mode Density